Work EX 4
(a) The x-component of the gravitational force is constant and points in the direction of the motion. Select the coordinate system as shown in the diagram below.
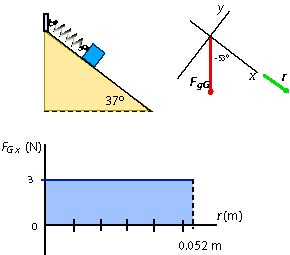
The x-component of the displacement is in this coordinate system. The x-component of the gravitational force is . Thus the work done by the gravitational force on the box is positive.
(b) The direction of the force of kinetic friction is opposite to the direction of the motion. To determine the force of kinetic friction we need to determine the normal force.
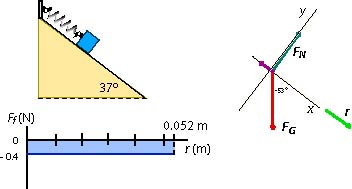
Write the equation for the y-components
The x-component of the frictional force is
The work done by friction
Note that we had to first find the normal force from the sum of the y-components of the forces acting on the box and then compute the magnitude of the force of kinetic friction. The work done by friction on the box is negative and it means that due to friction, the energy of the box decreased.
(c) The spring force is a linear function of the extension of the spring . In this case the displacement of the box is equal to the extension of the spring. The magnitude of the force of spring is . We note that the spring force acts opposite to the direction of motion and therefore the x-component of the spring force is negative. We need to plot the graph of the x-component of the spring force versus and use it to compute the work.
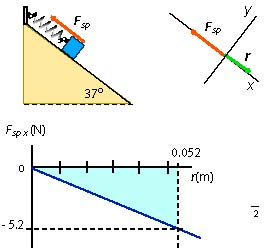
The work done is negative. It means that the box lost 0.135 J of energy due to the work done by the spring force.
(d) The total work is the sum of the work done by these three forces. We found that the total work is zero:











