Work EX 8
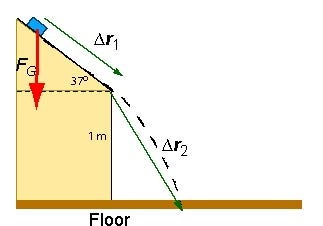
The mass has a total displacement
as is shown in the diagram below.
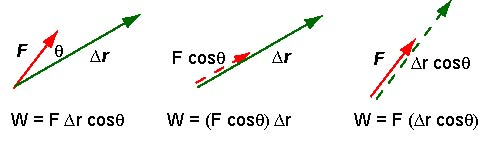
The work is done by a component of the force parallel to the displacement. But we can also conceptualize the work as a product of force and a component of the displacement that is parallel to the force. This second view is particularly useful in this problem. The diagram below shows that in each case the work done is the same.
To compute the work done by the gravitational force while sliding down the incline, we can compute the the component of the dislacement which is parallel to the force
and then compute the work:
(b) While the mass is falling, the force of gravity on the mass is constant and points vertically down. The acceleration of the box also points vertically down. The path of the box is a parabola (dashed line). The diagram shows the displacement of the box during the free fall and the component of the displacement which is parallel to the force. In this case, we don't know the magnitude of the displacement (although we can compute it by using the equations of kinematics if we want to). It is not necessary because we know that the component of the displacement parallel to the force is 1 m.
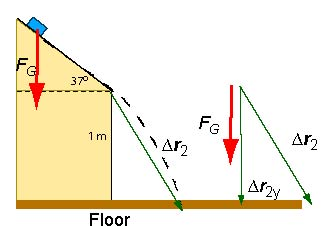
The work done by the gravitational force during the free fall is
(c) The work done by gravity for the entire motion is the sum of (a) and (b) (i.e.: 32 J)
