Linear Momentum and Collisions
Kreshnik Angoni
LINEAR MOMENTUM
- The observations on different situation of collision between two objects showed that one may model and explain the experimental results by use of a particular physical concept; the linear momentum
.....(1)
- m is mass and is the velocity of considered object.
- The linear momentum offers a very useful and more general way, to state the Newton’s second law:
.... (2)
Newton's 2nd Law: “The net force acting on a particle is equal to the rate of change of its linear momentum”
If the mass of object remains constant during the observation (common situation) the eq.(2) transforms to
the classic form
......(3)
But the equation (3) cannot describe the motion if the mass of object changes during the observation
(reactive motion of rockets). Meanwhile the equation (2) does include those situations, too.
CONSERVATION OF LINEAR MOMENTUM
- In one of the first relevant experiments about the linear momentum, it was found that when two isolated bodies ( net external force over them is zero) collide and stick together (figure 1), the total linear momentum before and after collision is the same, i.e
(before collision) (after collision) ...... (4)
Further experiments proved that this is a particular application of a general mechanics principle: the conservation of linear momentum.
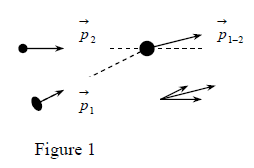
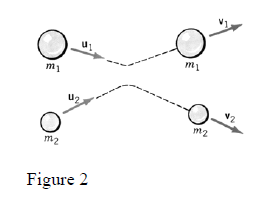
- One considers the collision between two particles with masses and with velocities
, before the collision and ,
after the collision (Fig.2).
Note that the collision (type of interaction) happens during a real touch of particles (like billiard balls) or during a no-touch repeal of particles (like two electrical charges of the same sign).
In general, there is a change of each particle linear momentum after a collision type interaction.
In order to calculate these changes, one uses the Conservation of Linear Momentum Principle, which states that:
The total linear momentum of a system of particles remains constant
if the external force exerted on the system is zero.
, or .....(5)
The application of this law in the case of two particles’ collision gives:
........ (6)
The vector equation (6) includes three conservation conditions, one for each velocity component
......(7)
The equations (7) show that when the linear momentum is conserved, each of its components is independently conserved.
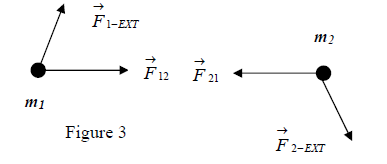
- When does the principle of linear momentum conservation apply? One must remember that, in order to apply the principle of linear momentum conservation, the net external force acting on the system must be zero. To explain “why” we will consider the system of two particles with masses and .
- The internal forces acting on this system are exerted on particle (1) from the particle (2) and exerted on particle (2) from particle(1). The third law of mechanics states that:
.....(8)
Applying the equation (2) for the motion of particle (1) we get
.....(9)
and similarly for the particle (2)
.....(9)
Taking the sum of equations (9) and (10) we have
which gives:
.... (11)
where is the sum of external forces acting on each of particles of system and is the sum of linear momentums for all system particles.
Now, if the net external force acting over the system is zero, from eq(11) we get:
= constant ..... (12)
In the case of two particles, the equation (11) becomes:
The eq(12) holds on as long as there is no external action over the system.
- For cases when the ≠ 0, we deal with a vector along a direction in space.
- This vector has no components (i.e. = 0 ) over a plane perpendicular to its direction.
- So, one may select the Ox, Oy axes on this plane and apply the two first equations of system (6) because they hold on independently.
It comes out that, even when ≠ 0, the components of linear momentum of system along the directions perpendicular to are conserved. So,this principle has a wide range of applications.
TYPES OF COLLISIONS
-The principle of linear momentum conservation is very general. It applies in all fields of physics,
mechanical collisions, explosions, reactive motion, light emission/absorption, nuclear decay and
nuclear reactions. So, it is important to clarify some basic issues related to term “collisions”.
- In physics, one uses the term collision when talking about “ a brief and strong interaction between
two or more bodies”.
What does one considers as a brief time of interaction?
This parameter ( Δt ) depends on the considered phenomena; for mechanical collisions (like balls, cars, people, objects) a
collision lasts (Δt ) from 0.001s to 1 s. A collision between elementary particles lasts (Δt ) for about
10-23s. In the case of galaxies a collision lasts (Δt =) about several millions of years.
- There are two types of collisions: elastic and inelastic.
In both cases the total linear momentum of the system is conserved if no external forces are present.
The distinction concerns the total KINETIC energy of the system.
In ELASTIC collisions, the total KINETIC energy of the system is conserved too.
So, there are two equations that apply for elastic collisions.
In the case of two particles’ elastic collision one gets:
....(13)
Note that during an elastic collision, the kinetic energy of the system is transformed (partially or
completely) into potential elastic energy but after the collision (after Δt) it is completely recovered into
kinetic energy of the system. The elastic collisions are common phenomena in atomic or nuclear
physics. In everyday life there are no really elastic collisions; even the collision between hard steel
balls is close but not exactly elastic.
- In an inelastic collision the total kinetic energy of the system is not conserved. In a completely
inelastic collision, the bodies stick together after collision.
In general, during an inelastic collision a part of kinetic energy of the system is transformed into potential elastic energy and the other part into thermal, internal energy, sound and even light.
It is important to underline that this second part does not recover into kinetic energy of system particles after the collision.
ELASTIC COLLISION IN ONE DIMENSION
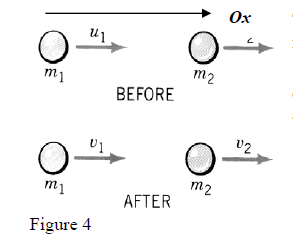
-The figure 4 presents the collision of two particles with masses , . They have initial velocities , along the same space direction that we select as Ox axis.
We consider “a central collision” that leaves the motion of particles along the same space direction, i.e. their velocities after collision , are along Ox axis too.
So, , , , ..... (14)
To simplify the picture, all velocities are shown directed at one sense but for the collision to happen one must have > > or > 0 and < 0 which is something that appears at algebraic values of components.
As this is an elastic collision, the two conservation laws apply. By projecting the equations (13) on Ox axis, one gets:
...... (15)
...... (16)
We rewrite eq. (16) in form
..... (17)
Then we divide eq.(17) by eq.15 and get:
.......(18)
The relation (18) shows that in 1-D elastic collisions, the amplitude of relative velocity of second particles versus first particle remains the same but its direction is reversed.
- Ex_1. Find , for the central collision of two particles with equal masses( i.e. ≡ m ).
In this case eq.(5) becomes:
On Ox ....... (19)
From two eq.(18-19) one can find easily that
and ..... (20)
If before the collision the target (particle 2) is at rest, = 0; ≠ 0,
it follows that, after collision
i.e. the first particle stops moving and
i.e. the second particle moves with the velocity of the first particle before collision.
One sees this situation often in billiard games.
- Ex_2. Find , for the central collision of two particles with unequal masses ( ≠) when the target is at rest(; ≠ 0).
In this case eq.(5) gives on Ox axis
........ (21)
while the equation (18) transforms to
......(22)
The solution of system (21-22) gives
and ......(23)
The expressions (23) simplify essentially in the following situations:
• When >> , it comes out that ≈ and ≈ i.e.
the first particle maintains its initial velocity but the second one imparts with the double of u1.
This is a common situation when a golf club () gives a central hit to a golf ball ().
• When << , it comes out that ≈ - and ≈ 0
i.e. the first particle reverses the sense but keeps the same magnitude of velocity.
This would correspond to the situation when a ping-pong ball hits centrally a bowling ball.
IMPULSE
- Often we have to consider “impulsive actions” i.e. actions that last for a very short interval of time. A
specific physical quantity, the impulse vector is used to study these situations.
If the linear momentum of a particle (body) changes from to ,
, one says that the impulse is exerted on the particle:
...... (24)
Note that impulse is a vector and its unit is [kg*m/s].
Its magnitude and direction are defined by the difference of vectors and .
-As impulse and the force exerted on the particle are expressed through the changes of particle linear momentum, there is a relation between them, too. From the “modern expression” of the second law
we get:
.......(25)
which is a differential expression.
The finite change of linear momentum Δ during time interval [ti, tf] is calculated as the sum of
elementary vectors and for this type of calculations one uses the integral procedures.
..... (26)
If we consider 1-D problems, ,, have the same direction and the expression (26) transforms to:
..... (27)
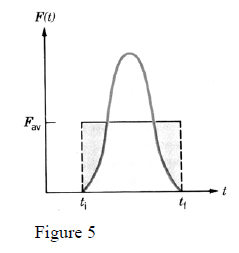
-Without going into details, the integral (27) is equal to the surface under the graph F = F(t) shown in figure 5.
The relation (27) is valid for all possible form of force evolution in time but it is mainly used in case of impulsive
forces.
An impulsive force acts during a short interval of time
during which it increases and decreases abruptly.
During this short interval, the action of impulsive force is much bigger than other forces exerted on the particle. So,
one neglects the effect of other forces when an impulsive force is in action.
In these circumstances, although F in (27) stands for the net force exerted over the particle, only the
impulsive force is counted under integral at formula (26). This is known as the impulsive approximation.
Example: The impulsive force exerted on a ball during the short time interval a player
kicks the soccer ball is much bigger than its weight and it is this force ,
that decides about the change of linear momentum of the ball.
Only this force is included under the integral (26).
-The problem with impulsive forces is that, in general, we do not know the analytic function F = F(t)
that describes its evolution in time. That’s why, instead of the real force, one operates with an average
(constant) force acting during the time interval Δt (fig.5) such that its impulse be I .
We get then
.......(28)
Note that the equity of expressions (27, 28) graphically means that the area under the graph F = F(t) is
equal to the area of rectangle with base Δt and height .
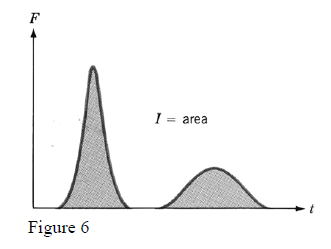
The graphical visualisation of the impulse serves as a good reference to understand that a given change of particle linear momentum needs the application of a given impulse and this can be achieved in two different ways (see figure 6) ; by use of a large force applied briefly or by use of a weaker force applied for a long interval of time.
This kind of information is important to keep in consideration in situations when:
• The exertion of a very large force for a short interval of time can create problems for the stability of the system.
• There is a limited flexibility about the production of large forces.
• A little bit longer Δt interaction time does not affect essentially the expected effect.