RC Circuits: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[ | Back to [[Electricity_and_Magnetism]] | ||
= Textbook = | = Textbook = | ||
*[https://openstax.org/books/university-physics-volume-2/pages/10-5-rc-circuits University Physics Volume 2: Chapter 10.5 - RC Circuits] | *[https://openstax.org/books/university-physics-volume-2/pages/10-5-rc-circuits University Physics Volume 2: Chapter 10.5 - RC Circuits] | ||
= What is a Capacitor and what is Capacitance = | = What is a Capacitor and what is Capacitance = | ||
See [[Capacitors]] | |||
== Capacitor | = RC Circuits = | ||
During the | == Capacitor Charging (Voltage over Time) == | ||
<math> V(t) = V_0 e^{-\frac{t}{RC}} </math> | [[File:Charging.png|right|400px]] | ||
During charging, the voltage across a capacitor increases exponentially, approaching its final value. | |||
<math> V(t) = V_0 \left( 1 - e^{-\frac{t}{RC}} \right) </math> | |||
*Where:* | *Where:* | ||
* *V(t)* is the voltage at time t (in volts, V) | * *V(t)* is the voltage at time t (in volts, V) | ||
* *V_0* is the | * *V_0* is the final voltage (in volts, V) | ||
* *R* is the resistance (in ohms, Ω) | * *R* is the resistance (in ohms, Ω) | ||
* *C* is the capacitance (in farads, F) | * *C* is the capacitance (in farads, F) | ||
* *t* is time (in seconds, s) | * *t* is time (in seconds, s) | ||
== Capacitor | |||
During | == Capacitor Discharge (Voltage over Time) == | ||
<math> V(t) = V_0 | [[File:Discharging.png|right|400px]] | ||
During the discharge of a capacitor through a resistor, the voltage decreases exponentially over time. | |||
<math> V(t) = V_0 e^{-\frac{t}{RC}} </math> | |||
*Where:* | *Where:* | ||
* *V(t)* is the voltage at time t (in volts, V) | * *V(t)* is the voltage at time t (in volts, V) | ||
* *V_0* is the | * *V_0* is the initial voltage (in volts, V) | ||
* *R* is the resistance (in ohms, Ω) | * *R* is the resistance (in ohms, Ω) | ||
* *C* is the capacitance (in farads, F) | * *C* is the capacitance (in farads, F) | ||
* *t* is time (in seconds, s) | * *t* is time (in seconds, s) | ||
== Example Graphs == | |||
[[File:RC example graph.png|left|400px]] | |||
<br class="clear"/> | |||
<div style="clear:both;"></div> | |||
= Videos = | |||
<youtube>vT6uonSYS9U</youtube> | |||
<youtube>Fjzy6cHNn6w</youtube> | |||
= Simulations = | = Simulations = | ||
*[http://phet.colorado.edu/en/simulation/circuit-construction-kit-ac-virtual-lab PhET Circuit Construction Kit] | |||
| Line 42: | Line 52: | ||
<br class="clear"/> | <br class="clear"/> | ||
Back to [[Electricity_and_Magnetism]] | Back to [[Electricity_and_Magnetism]] | ||
<br class="clear"/> | |||
Next: [[Magnetic Fields]] | |||
Latest revision as of 15:50, 22 November 2024
Back to Electricity_and_Magnetism
Textbook
What is a Capacitor and what is Capacitance
See Capacitors
RC Circuits
Capacitor Charging (Voltage over Time)
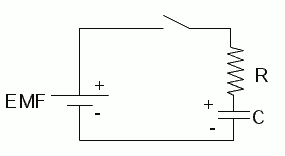
During charging, the voltage across a capacitor increases exponentially, approaching its final value.
- Where:*
- *V(t)* is the voltage at time t (in volts, V)
- *V_0* is the final voltage (in volts, V)
- *R* is the resistance (in ohms, Ω)
- *C* is the capacitance (in farads, F)
- *t* is time (in seconds, s)
Capacitor Discharge (Voltage over Time)
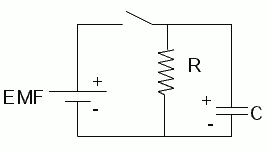
During the discharge of a capacitor through a resistor, the voltage decreases exponentially over time.
- Where:*
- *V(t)* is the voltage at time t (in volts, V)
- *V_0* is the initial voltage (in volts, V)
- *R* is the resistance (in ohms, Ω)
- *C* is the capacitance (in farads, F)
- *t* is time (in seconds, s)
Example Graphs
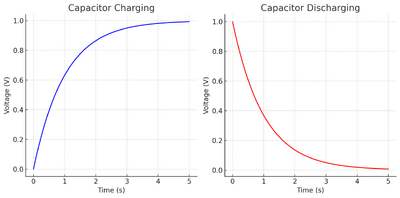
Videos
Simulations
Other Links
Back to Electricity_and_Magnetism
Next: Magnetic Fields