Newtons Laws EX 2
First we focus on the mass kg. There are four forces acting on this particle: , , , and pointing towards the string pulling the block. The particle moves down the incline and therefore the force of friction points up the incline. Similarly, we list forces on the mass kg. The force of tension pulls the block towards the left.
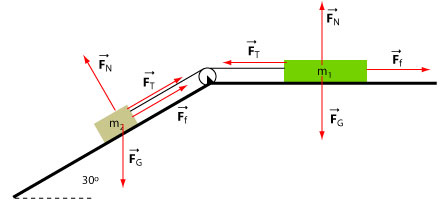
The blocks move at constant velocity and therefore their acceleration is zero. We select the x-axis parallel to the incline and parallel to the horizontal surface as shown in the diagram below.
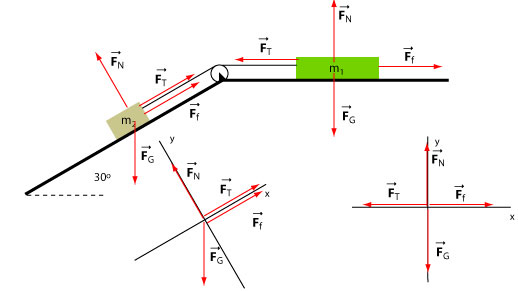
We will deal with each particle separately. First we focus on the mass kg. The gravitational force points vertically down and therefore it makes a 30° angle with the negative y-axis; consequently, it makes an angle -120° with the positive x-axis.
The components of the forces exerted on are:
| Forces | x-component | y-component |
|---|---|---|
| mg cos(-120°) = 50 cos(-120°) = -25 N | 50 sin(-120°) = -43 N | |
| 0 | ||
| 0 | ||
| 0 |
Note that we used in our computations.
First we have to deal with the y-component:
This yields N
Now we can proceed to think about the x-component. Using that the acceleration is 0, we can write:
We cannot solve this equation immediately, and so, we focus on the mass kg.
The components of the forces exerted on are:
| Forces | x-component | y-component |
|---|---|---|
| 0 | -100 N | |
| 0 | ||
| 15 N | 0 | |
| 0 |
First we have to deal with the y-component:
This yields N.
Now we can proceed to think about the x-component, and because acceleration is 0, we can write:
There remains only to solve the following system of two equations:
Solving for , we find N and solving for we find N.