Newtons Laws EX 30

We will deal with each particle separately. First we focus on the mass $m_{2}=5$ kg.

There are four forces acting on this particle: $F_{G_{2}}$, $F_{N_{2}}$, $F_{f_{2}}$, $F_{T}$. Note that the tension acting on both particles is the same. The particle moves down the incline and therefore the force of kinetic friction points up the incline.

The particle moves at constant velocity and therefore the acceleration is zero and both components of the net force are also zero. We select the x-axis parallel to the incline and draw the free-body diagram.

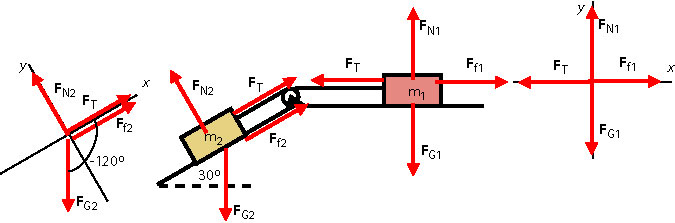
The components of the forces exerted on $m_{2}$ are:

Forces	x-component	y-component
$F_{G_{2}}$	50 cos(-120°) = -25 N	50 sin(-120°) = -43 N
$F_{N_{2}}$	0	$F_{N_{2}}$
$F_{f_{2}}$	$F_{f_{2}}$	0
$F_{T}$	$F_{T}$	0

Note that we will use $g=10m/s^{2}$ in our computations.

First we have to deal with the y-component:

$-43+F_{N_{2}}=0$

This yields $F_{N_{2}}=43$ N. Substituting this result into the equation for the force of kinetic friction we get:

$F_{f_{2}}=\mu _{K}F_{N_{2}}=43\mu _{K}$

Now we can proceed to think about the x-component. Using that the acceleration is 0, we can write:

$F_{T}+43\mu _{K}-25=0$

Now we focus on the mass $m_{1}=3$ kg.

There are four forces acting on this particle: $F_{G_{1}}$, $F_{N_{1}}$, $F_{f_{1}}$, $F_{T}$. The particle moves to the left and therefore the force of kinetic friction points to the right and is parallel to the surface.

The particle moves at constant velocity and therefore the acceleration is zero and both components of the net force are also zero. We will select the x-axis parallel to the horizontal. (See the diagram above.)

The components of the forces exerted on $m_{1}$ are:

Forces	x-component	y-component
$F_{G_{1}}$	0	-30
$F_{N_{1}}$	0	$F_{N_{1}}$
$F_{f_{1}}$	$F_{f_{1}}$	0
$F_{T}$	$-F_{T}$	0

First we have to deal with the y-component:

$-30+F_{N_{1}}=0$

This yields $F_{N_{1}}=30$ N. Substituting this result into the equation for the force of kinetic friction we get:

$F_{f_{1}}=\mu _{K}F_{N_{1}}=30\mu _{K}$

(Note: Both blocks have the same coefficient of kinetic friction and therefore we use the same symbol in the case of both masses.)

Now we can proceed to think about the x-component, and because acceleration is 0, we can write:

$-F_{T}+30\mu _{K}=0$

It thus remains to solve the following system of two equations:

$F_{T}+43\mu _{K}-25=0$
$-F_{T}+30\mu _{K}=0$ 

Adding these equations gives:

$43\mu _{K}+30\mu _{K}-25=0$

Solving for $\mu _{K}$, we find $\mu _{K}=0.34$

By substituting $\mu _{K}$ in the first equation we can solve for $F_{T}$, and find that $F_{T}=10.2$ N.