Newtons Laws EX 40
A satellite on its way to the Moon is attracted towards the Earth with a gravitational force of . The force gradually decreases as the distance, , between the Earth and satellite increases. At the same time the Moon attracts the satellite with a gravitational force (which increases as the distance to the Moon decreases.) These two forces oppose one other (see the diagram below).
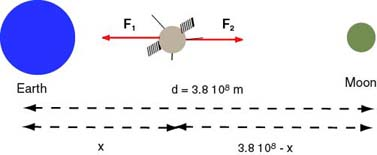
The distance between the Earth and the Moon is m. When the satellite is at a distance from the Earth then it is at a distance from the Moon. We are looking for a distance at which , which happens when the magnitudes of these forces are equal. The gravitational force depends on the mass of the Earth, the mass of the satellite, and the distance between them; the force depends on the mass of the Moon , the mass of the satellite, and the distance . We will now write the equation and replace both and by appropriate formulas in the Newton Law of gravitation.
Given that the Earth is 81 times more massive than the Moon, we can write: . Upon substitution into the above, we get:
The constants , and cancel out to leave us with:
By taking the positive square root on either side of this equation, we get
and after cross multiplication and isolation of , we see that m.