Newtons Laws EX 44

We will consider each particle as a system (meaning that we will deal with each particle separately.) Assume that the pulley and the string are massless and that there is no friction on the pulley. Therefore, we can consider that the tension in the string is constant. Consequently, the magnitude of $F_{T}$ is the same for both masses.

The forces acting on $m_{1}$ are $F_{G}$ and $F_{T}$. The forces acting on $m_{2}$ are $F_{G}$, $F_{N}$, $F_{f}$ and $F_{T}$. The normal force and force of friction are acting on this object because it is in contact with a surface. The direction of the kinetic friction depends on the direction of motion:

(a) The mass $m_{1}$ moves down and therefore $m_{2}$ moves uphill. The force of friction points down the hill. The force diagram is shown below:

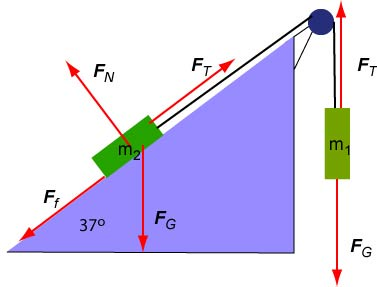
The acceleration probably points uphill. We make this guess by comparing the force of gravity acting on $m_{2}$ and $m_{1}$. While $m_{2}$ (5 kg) is partially supported by an incline while $m_{1}$ (5 kg) is freely suspended. Thus, the gravitational force on $m_{1}$ should have a greater impact on the motion of these objects than the gravitational force on $m+2$. In any case, it is evident that the acceleration of $m_{2}$ is parallel to the incline and the acceleration of $m_{1}$ is vertical. The diagram below shows the free body diagrams and the chosen coordinate systems for each of the two particles. In view of our guess, we will assume that the acceleration is positive.

The figure below shows these forces and free body diagrams for both particles.

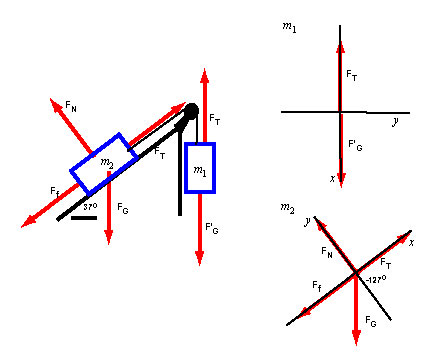
Focus on the free body diagram labelled $m_{2}$: The components of the forces exerted on $m_{2}$ are:

Forces	x-component	y-component
$F_{G}$	50 cos(-127°) = -30 N	50 sin(-127°) = -40 N
$F_{N}$	0	$F_{N}$
$F_{f}$	$-F_{f}$	0
$F_{T}$	$F_{T}$	0

Note that we used $g=10m/s^{2}$ in our calculations.

We deal first with the y-component:

$-40+0+0+F_{N}=0$

This yields $F_{N}=40$ N. We apply the equation for the force of kinetic friction and get:

$F_{f}=\mu _{K}F_{N}=(0.25)(40)=10$ N

Now we write the equation for the x-component:

$-30-10+F_{T}+0=5a$

We cannot solve this equation. First, we need to consider the other particle.

The forces exerted on $m_{1}$ are $F_{G}$ and $F_{T}$. Friction and the normal force don't enter into consideration because this object is not in contact with any surface. Its acceleration probably points downward. We have to assign the direction of axis so that our choice is consistent with the choice we have made for $m_{2}$. Because of this, we orient the positive x-axis pointing downward. Refer to the free body diagram above. Note that we only need to be concerned with the components along the x-axis.

The components of the forces exerted on $m_{1}$ are:

Forces	x-component
$F_{G}$	50 N
$F_{T}$	$-F_{T}$

We write the equation for the x-component:

$50-F_{T}=5a$

We have two equations in two unknowns:

$50-F_{T}=5a$
$-30-10+F_{T}=5a$

Adding these equations gives

$-30-10+50=10a$

and solving for $a$, we get that $a=1m/s^{2}$. Note that acceleration is positive, indicating that our guess was right!

Substituting this value into the first equation and solving for $F_{T}$, we get $F_{T}=45$ N.

(b) In this case, the block $m_{1}$ moves up and so the block $m_{2}$ moves down the hill. The only difference between these two cases is that the direction of the force of friction changes and in this case points up the hill. We can keep the same axis as we did before. The magnitude of friction will be the same. It will only change sign. Thus, we can write the two equations:

$50-F_{T}=5a$
$-30+10+F_{T}=5a$

Adding these equations gives

$-30+10+50=10a$

and solving for $a$, we get that $a=3m/s^{2}$. Note that acceleration is still positive, indicating that our guess was right! Solving the equation for the tension, we find

$50-F_{T}=5(3)$

$F_{T}=35$ N

(c) Now, the block $m_{1}$ moves up at constant velocity and so the block $m_{2}$ moves down the hill at constant velocity. The acceleration of both systems is zero. We will redraw the diagrams.

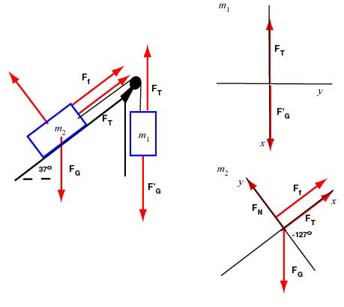
We can compute the components of forces exerted on $m_{2}$ first:

Forces	x-component	y-component
$F_{G}$	$10m_{2}\cos(-127^{\circ })=-6m_{2}$	$10m_{2}\sin(-127^{\circ })=-8m_{2}$
$F_{N}$	0	$F_{N}$
$F_{f}$	$-F_{f}$	0
$F_{T}$	$F_{T}$	0

We deal first with the y-component:

$-8m_{2}+0+0+F_{N}=0$

This yields $F_{N}=8m_{2}$. We apply the equation for the force of kinetic friction and get:

$F_{f}=\mu _{K}F_{N}=(0.25)(8m_{2})=2m_{2}$

Now we write the equation for the x-component:

$-6m_{2}+2m_{2}+F_{T}+0=0$

We cannot solve this equation. First, we need to consider the other particle.

The components of the forces exerted on $m_{1}$ are:

Forces	x-component
$F_{G}$	60 N
$F_{T}$	$-F_{T}$

We write the equation for the x-component:

$60-FT=0$

The last equation yields $F_{T}=60$ N.

Substituting $F_{T}$ into the equation that we had before for the x-components of forces acting on $m_{1}$, we obtain

$-6m_{2}+2m_{2}+60+0=0$

Solving for $m_{2}$ we get that $m_{2}=15$ kg.