Work-Energy Theorem EX 3
Before we can find the work done, we must find the forces acting on the body. We start by drawing a free-body diagram for the forces acting on the block and include the displacement:
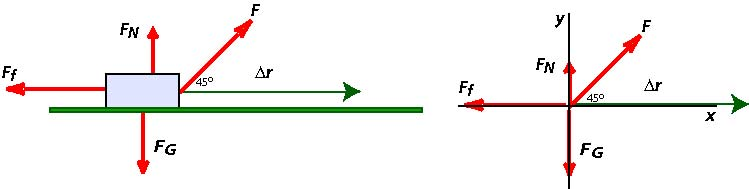
- The force F makes an angle of 45° with the displacement. It is a constant force and therefore we can write . Note that at this point we cannot determine the value of the work done by because we don't know the magnitude of .
- To compute the work done by friction, we must first determine the force of friction. We will use the the y-component of forces and Newton's Second Law to find .
Solving for we find
Consequently, the force of friction is
Then the work done by friction is
We still could not find the value of this work because we don't have the magnitude of . - The work done by gravity is zero because the displacement is perpendicular to the gravitational force. On rereading the problem, we note that the speed is constant. This means that the kinetic energy does not change and therefore the net work is zero. We can use this information along with the fact that . Substituting into this equation the expressions that we found above, we get
Solving for , we get . We can then use this value to compute
as well as the value of the work done by friction: