Rotational Motion
Helena Dedic
Rotational Motion: Main Points
• Motion with constant angular acceleration
• Circular motion as one dimensional motion
- o The angular position describes a position of a particle on a circular path.
- o Units: rad (radians)
- o Note: the displacement is often described by a number of revolutions (rev)
rad
- o The angular displacement: the change of position of a particle is related to the length of the path (arc) travelled by the particle:
- o The angular displacement is positive if the particle moves in a counterclockwise direction and it is negative if the particle moves in a clockwise direction.
• Introduction of angular velocity:
- o Definition:
- o Units: rad/s and rpm
- o Conversion of units:
- o Since the speed is constant in uniform circular motion, the angular velocity is also constant and we can write:
where T is the period of the circular motion.
- o Relationship between the angular velocity and the speed of the particle:
- o Relationship between angular velocity and radial acceleration:
• In the context of circular or rotational motion, the acceleration a as you know it from kinematics is called linear acceleration so as to distinguish it from the angular acceleration which we are about to introduce. In the previous sections we used the cartesian coordinate system of axis to determine the components of the linear acceleration vector. In the context of circular or rotational motion it is useful to use a system of axis parallel to the radius and parallel to the tangent of the circle:
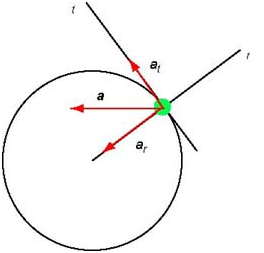
The two components are called radial acceleration and tangential acceleration . Since this system of axis is related to the circular path we are taking advantage of the fact that the particle moves along the circle. Note that in this system a particle in uniform circular motion has and the acceleration has only one non-zero component.
We say that a particle is in non-uniform circular motion if its speed varies. Note that the velocity always points along the tangent to the path. Thus, when the speed varies the particle has a non-zero tangential component of acceleration:
It is important to remember that the acceleration has two components: an always present radial acceleration and a tangential acceleration (only when the speed varies).
• Introduction of angular acceleration
- o When a particle is in non-uniform circular motion its angular velocity also varies. The rate of change of the angular velocity is called angular acceleration:
- o Units: or rad/s/s e.g., 3 rad/s/s implies that the angular velocity increases 3 rad/s every second.
- o The relationship between angular acceleration and tangential acceleration:
- o Since the angular acceleration is constant the graph is a straight line with a slope equal to \alpha. We can use this graph to solve problems involving motion with constant angular acceleration.
- o We can also use similar equations as we used to solve problems involving motion with constant acceleration in one dimension:
Exercises
Exercise 1
At t = 0 a flywheel is rotating at 50 rpm. A motor gives it a constant acceleration of until it reaches 100 rpm. The motor is then disconnected and the flywheel rotates at constant angular velocity. How many revolutions are completed at t = 20 s?
Solution:
First, we convert the angular velocity to rad/s:
It accelerates with an angular acceleration:
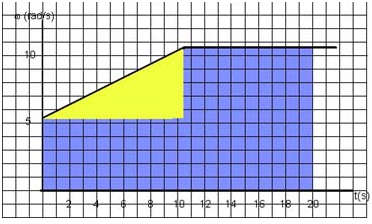
The acceleration lasts until the angular velocity reaches 10.46 rad/s. After that the rotor continues to spin with constant angular velocity. We can sketch the w - t graph. It begins at 5.23 rad/s. The graph is a straight line with slope 0.5 rad/s/s. When the angular velocity reaches 10.46 rad/s the graph becomes a horizontal line. See the graph below:
To determine the angle through which the rotor turns we have to determine the area under the graph. First we need to know when the rotor reaches the angular velocity of 10.46 rad/s.
Therefore the flywheel moves at constant angular velocity for 20 - 10.46 = 9.54 s. The angular displacement is equal to the total area is the area of a triangle plus the area of two rectangles: ½ × 5.23 × 10.46 + 5.23 × 10.46 + 10.46 × 9.54 = 182 rad.
Now we have to convert the angular displacement in rads to revolutions:
.
Exercise 2
A wheel starts from rest and accelerates uniformly. As the rate of rotation changes from 20 to 50 rpms the wheel makes 40 revolutions. Find the angular acceleration and the number of revolutions completed by the time the wheel reaches 20 rpms.
Solution:
The wheel starts from rest with a constant angular acceleration.
At some time the wheel rotates at .
later the wheel rotates at . What is the angular acceleration?
For this kind of problems (given two angular velocities and the angular displacement) we should use the last equation of kinematics:
Substituting into this equation we find
Solving for we find .
We can use the same equation to find the angular displacement from the beginning until the angular velocity becomes 2.1 rad/s:
Solving for we find .