$$
\newcommand{\norm}[1]{\left\Vert#1\right\Vert}
\newcommand{\abs}[1]{\left\vert#1\right\vert}
\newcommand{\set}[1]{\left\{#1\right\}}
\newcommand{\Comp}{\mathbb C}
\newcommand{\Real}{\mathbb R}
\newcommand{\Nat}{\mathbb N}
\newcommand{\of}[1]{\left ( #1 \right ) }
\newcommand{\To}{\rightarrow}
\newcommand{\eps}{\varepsilon}
$$
Integral Calulus lecture notes: Area under a curve - introductory examples
Eugene Kritchevski, Vanier College, August 25, 2016
To view some of the interactive features of this document you may need to install the CDF player and browser plugin on your computer:
link to download and install.
The method of Riemann sums for computing the area under the graph of a function
One can use elementary geometry to compute the area of a region built from rectangles, triangles or disks. How can we compute the area of a region delimited by more general curves? A possible approach is to accurately approximate the region by rectangles. We first illustrate the method with examples and then describe the general procedure.
Example 1: the area of region under $y=x^2$ from $x=0$ to $x=1$
Consider for instance the region delimited by the parabola $y=x^2$, the $x$-axis, and the vetrical lines $x=0$ and $x=1$. We sometimes say informally "The region under $y=x^2$ from $x=0$ to $x=1$".
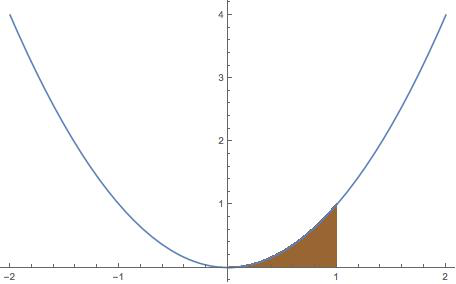
The strategy for computing the area is to approximate the region with rectangles. The animation below shows two possible approximation methods.
- What is the meaning of the parameter $n$?
- How are the approximations are constructed?
- Which one is the lower estimate and which one is the upper estimate?
- Reproduce the calculation for the lower and for the upper estimates for $n=5$.
- Do the lower an the upper estimates look very different when $n$ gets larger?
- Guess the exact area under $y=x^2$ from $x=0$ to $x=1$.
How can we compute the exact area under $y=x^2$ from $x=0$ to $x=1$ without a computer? A possible approach is to find an explicit expression for $R_n$ or for $L_n$ and then study this expression as $n$ gets large.
Let us now compute an explicit formula for $R_n$ for an arbitrary $n$. There are in total $n$ approximating rectangles.
Each approximating rectangle has base $\frac{1}{n}$ and the heights are
$$\of{\frac{1}{n}}^2, \of{\frac{2}{n}}^2,\of{\frac{3}{n}}^2,\cdots,\of{\frac{n}{n}}^2.$$
The areas of the the approximating rectangles are then
$$\frac{1}{n}\cdot\of{\frac{1}{n}}^2, \frac{1}{n}\cdot\of{\frac{2}{n}}^2,\frac{1}{n}\cdot\of{\frac{3}{n}}^2,\cdots,\frac{1}{n}\cdot\of{\frac{n}{n}}^2.$$
Summing these up, we get
$$R_n=\frac{1}{n}\cdot\of{\frac{1}{n}}^2+\frac{1}{n}\cdot\of{\frac{2}{n}}^2+\frac{1}{n}\cdot\of{\frac{3}{n}}^2+\cdots+\frac{1}{n}\cdot\of{\frac{n}{n}}^2.$$
Let us simplify the expression for $R_n$ using basic algebra and the summation formula (in expanded form) for sums of squares of positive integers.
$$
\begin{split}
R_n&=\frac{1}{n}\cdot\left[\of{\frac{1}{n}}^2+\of{\frac{2}{n}}^2+\of{\frac{3}{n}}^2+\cdots+\of{\frac{n}{n}}^2\right]\\
&=\frac{1}{n}\cdot\frac{1}{n^2}\cdot\left[1^2+2^2+3^2+\cdots +n^2\right]\\
&=\frac{1}{n^3}\cdot\left[ \frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6}\right]\\
&=\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}\\
&\\
\end{split}
$$
For instance,
$$R_{10}=\frac{1}{3}+\frac{1}{20}+\frac{1}{600}=0.385$$
$$R_{100}=\frac{1}{3}+\frac{1}{200}+\frac{1}{60000}=0.33835$$
$$R_{1000}=\frac{1}{3}+\frac{1}{2000}+\frac{1}{6000000}=0.3338335$$
As $n$ gets very large, the terms $\frac{1}{2n}$ and $\frac{1}{6n^2}$ get very close to $0$ and therefore $R_n$ gets very close to $\frac{1}{3}$. We write
$$\lim_{n\To\infty} R_n =\frac{1}{3}.$$
A similar analysis holds for $L_n$. We have
$$
\begin{split}
L_n&=\frac{1}{n}\cdot\of{\frac{0}{n}}^2+\frac{1}{n}\cdot\of{\frac{1}{n}}^2+\frac{1}{n}\cdot\of{\frac{2}{n}}^2+\cdots+\frac{1}{n}\cdot\of{\frac{n-1}{n}}^2\\
&=\frac{1}{n}\cdot\frac{1}{n^2}\cdot\left[0^2+1^2+2^2+\cdots +(n-1)^2\right]\\
&=\frac{1}{n^3}\cdot\left[1^2+2^2+\cdots +(n-1)^2+n^2-n^2\right]\\
&=\frac{1}{n^3}\cdot\left[\frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6}-n^2\right]\\
&=\frac{1}{n^3}\cdot\left[\frac{n^3}{3}-\frac{n^2}{2}+\frac{n}{6}\right]\\
&=\frac{1}{3}-\frac{1}{2n}+\frac{1}{6n^2}\\
&\\
\end{split}$$
For instance,
$$L_{10}=\frac{1}{3}-\frac{1}{20}+\frac{1}{600}=0.285$$
$$L_{100}=\frac{1}{3}-\frac{1}{200}+\frac{1}{60000}=0.32835$$
$$R_{1000}=\frac{1}{3}-\frac{1}{2000}+\frac{1}{6000000}=0.3328335$$
Again, as $n$ gets very large, the terms $\frac{1}{2n}$ and $\frac{1}{6n^2}$ get very close to $0$ and therefore $L_n$ gets very close to $\frac{1}{3}$. We write
$$\lim_{n\To\infty} L_n =\frac{1}{3}.$$
Let $A$ denote the the exact area under $y=x^2$ from $x=0$ to $x=1$. Then for each $n$
$$L_n \leq A \leq R_n.$$
Since $L_n$ and $R_n$ both approach $\frac{1}{3}$ as $n$ gets large, we conclude that $A=\frac{1}{3}$.
Note: Using the sigma notation, we can speed up calculations and reduce the amount of writing. For example, the calculation of $R_n$ can be compactly written as
$$R_n=\sum_{i=1}^{n}\frac{1}{n}\cdot\of{\frac{i}{n}}^2=\sum_{i=1}^{n}\frac{i^2}{n^3}=\frac{1}{n^3}\sum_{i=1}^{n}i^2=\frac{1}{n^3}\cdot\left[ \frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6}\right]=\frac{1}{3}+\frac{1}{2n}+\frac{1}{6n^2}.$$
Example 2: the area of the region under $y=x^2$ from $x=1$ to $x=4$
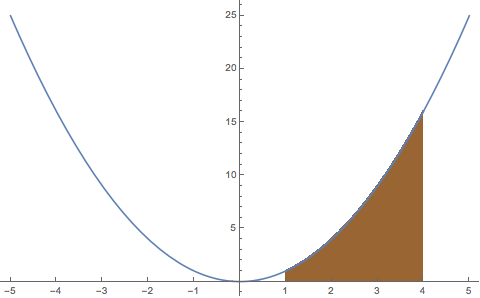
Again, we approximate the region by rectangles.
- What is the meaning of the parameter $n$?
- How are the approximations are constructed?
- What is the difference between the right endpoint and the left endpoint method?
- Which one is the lower estimate and which one is the upper estimate?
- Reproduce the calculation for the lower and for the upper estimates for $n=5$.
- Do the lower and the upper estimates look very different when $n$ gets larger?
- Guess the exact area under $y=x^2$ from $x=0$ to $x=1$.
To find the exact area $A$ of the region under $y=x^2$ from $x=1$ to $x=4$, we will first compute a formula for the right endpoint approximation $R_n$ for an arbitrary $n$ and simplify the expression for $R_n$ as much as possible.
Each approximating rectangle has base
$$\Delta x = \frac{4-1}{n}=\frac{3}{n}$$ and the heights are
$$\of{1+\Delta x}^2, \of{1+2\Delta x}^2,\of{1+3\Delta x}^2,\cdots,\of{1+n\Delta x}^2,$$
that is
$$\of{1+\frac{3}{n}}^2, \of{1+2\cdot\frac{3}{n}}^2,\of{1+3\cdot\frac{3}{n}}^2,\cdots,\of{1+n\cdot\frac{3}{n}}^2=4^2.$$
Summing the areas of the approximting reactangles, we get
$$R_n=\frac{3}{n}\cdot\of{1+\frac{3}{n}}^2+ \frac{3}{n}\cdot\of{1+2\cdot\frac{3}{n}}^2+
\frac{3}{n}\cdot\of{1+3\cdot\frac{3}{n}}^2 +\cdots +\frac{3}{n}\cdot\of{1+n\cdot\frac{3}{n}}^2.$$
The expression for $R_n$ is easier to handle with the sigma notation:
\begin{split}
R_n
&=\sum_{i=1}^{n}\frac{3}{n}\cdot\of{1+i\cdot\frac{3}{n}}^2\\
&=\sum_{i=1}^{n}\frac{3}{n}\cdot\of{1+\frac{6i}{n} +\frac{9i^2}{n^2} }\\
&=\sum_{i=1}^{n}\of{\frac{3}{n}+\frac{18i}{n^2} +\frac{27i^2}{n^3} }\\
&=\sum_{i=1}^{n}\frac{3}{n}+\sum_{i=1}^{n}\frac{18i}{n^2} +\sum_{i=1}^{n}\frac{27i^2}{n^3} \\
&=\frac{3}{n}\sum_{i=1}^{n}1+\frac{18}{n^2}\sum_{i=1}^{n}i +\frac{27}{n^3}\sum_{i=1}^{n}i^2 \\
&=\frac{3}{n}\cdot n+\frac{18}{n^2}\cdot\of{\frac{n^2}{2}+\frac{n}{2}} +\frac{27}{n^3}\of{\frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6}} \\
&=3+\frac{18}{2}+\frac{18}{2n} +\frac{27}{3} +\frac{27}{2n}+\frac{27}{6n^2} \\
&=21+\frac{45}{2n}+\frac{27}{6n^2} \\
&\\
\end{split}
As $n$ gets large, $21+\frac{45}{2n}+\frac{27}{6n^2}$ approaches $21$. We write
$$\lim_{n\to\infty} R_n=\lim_{n\to\infty}\of{21+\frac{45}{2n}+\frac{27}{6n^2}}=21$$
One could check that a similar computation for the left endpoint approximation $L_n$, would also give us $\lim_{n\to\infty} L_n=21$. For each $n$
$$L_n \leq A \leq R_n.$$
Both $L_n$ and $R_n$ both approach $21$ as $n$ gets large.
Therefore, the exact area $A$ of the region under $y=x^2$ from $x=1$ to $x=4$ area is $A=21$.
Exercise:
- Using the method of Riemann sums (use $R_n$), compute the area of the region under $y=x^2$ from $x=1$ and $x=2$
- Compute the area of the region under $y=x^2$ from $x=0$ to $x=4$, using the results of example 1 and example 2. The computation takes a few seconds - no need to use Riemann sums.
- Compute the area of the region under $y=x^2$ from $x=-1$ to $x=0$, using the result of example 1.
- Compute the area of the region under $y=x^3$ from $x=0$ to $x=1$, using Riemann sums (use $R_n$).

