Electric Potential Energy and Electric Potential
Kreshnik Angoni and Kevin Lenton
Worksheet.docx
Worksheet.pdf
Additional Problems
Other Resources:
- Haliday & Resnick, Fundamentals of Physics 21.1-5
- Openstax
- Printable version
Electric Potential and Electric Potential Energy are important extensions from the Electric Field, because they are scalar quantities, rather than vectors. For this reason they are very practical in examining the effects of charges on other charge.
Learning Objectives
After reading this page, watching the videos and reviewing the exercises, you will be able to:
- define potential energy and electric potential for a test charge in a uniform electric field.
- calculate the potential energy and electric potential for a small set of point charges.
- calculate the force as the derivative of a potential energy function in one dimension.
- calculate the field as the derivative of a potential function in one dimension.
- recognize conductors as regions of uniform potential.
A Short Review of Potential Energy (U)
The potential energy can be defined for a system only if conservative forces act between its constituents.
Conservative forces depend only on the position (not on speed or acceleration).
Only the difference between two values of potential energy (not the values by themselves) has a physical meaning. i.e. it is the relative value, not the absolute value that is important. This allows us to choose the location where potential energy is zero such that it simplifies the calculations. (Example; you might choose U = 0 for an object on the earth’s surface but if the object can move only inside the lab you should choose U=0 at floor level and you could even choose U=0 at the centre of the earth or at infinity if this choice simplifies the solution of considered problem. You are free to choose this reference because it is the value of potential energy relative to this reference position that is important.
The principle of energy conservation;
tells that, provided that the change in kinetic energy , the change of potential energy is equal to the work done by external forces.
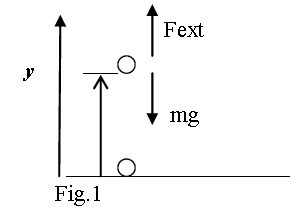
Consider an object (m) at rest on the surface of the earth; U(0) = 0. If we move it up “ slowly “and leave it at rest on a table of height y (fig.1), the object receives potential energy U(y) = mgy. The external force1 (the force you apply on it to make it move) would do a positive work Wext which increases the potential energy of the object (more correctly of the earth-object system).
Meanwhile, the internal conservative force (internal to the object-earth system that is, i.e. the weight), does the same amount of work but this is negative work. So,
What this means is the change in potential energy is equal to the work you do on the mass (the external work), but opposite in sign to the work that the force of gravity (the internal force) does in the same movement.
For an infinitesimal displacement dx, the internal force , does infinitesimal work equal to
The sign (-) in (3) shows that when a conservative force does positive work the potential energy decreases.
From (3) we get the relation between a conservative force and the potential energy
Ex: the Earth-object system; If the y direction is directed vertically up U(y) = mgy and
The potential energy of the object is actually the energy of the system earth-object and it is due to the gravitational field of the earth. You can define a function called the gravitational potential as the potential energy normalized for mass as described below.
Gravitational Potential VG is Gravitational Potential Energy Normalized for Mass
The gravitational potential at a location “h” of space is equal to the potential energy of a 1 Kg mass located at this point of the space. i.e. it is the potential energy normalized for mass.
Remember the gravitational potential energy is mgh.
Therefore
In this way you:
a) Define a function which is a characteristic of the earth's gravitational field.
b) For a mass m ≠1Kg, you get the equations
c) Can calculate the internal work done by gravitational field during the shift of a mass “m” inside it as
Definition of Electric Potential Energy for Point Charges
Consider one charge being brought towards another charge from infinity to a distance r.
The work done by you pulling the charges together will be equal to the increase in electric potential energy of the system.
Any other charges brought into this system will have to do work against the other charges, and so on as the charge distribution is assembled.
Note that the potential energy of the system increases if you do work bringing two positive charges together. However, the potential energy of the system decreases if you bring two opposite sign charges together: the charges want to rush together, and the potential energy is released as kinetic energy!
i.e. for electric potential energy, the signs of the charges should be included in the calculation.
Where to define the reference position U=0 ?
Remember that when dealing with gravitational potential energy, what is important is the change in potential energy, not the energy itself. This means that you can define where the potential energy is zero. You are free to define any position, but usually some points make better reference points than others. For instance, for gravitational potential energy, choosing the lowest point in the problem as the reference (U=0) is recommended.
For electric potential energy of point charges, it is recommended to choose infinity as the reference position. The electric force is zero at infinity, anyway, so that makes sense.
For something like a capacitor, which has zero field outside the plates, the reference position could be on the negatively charged plate. In this way the positive plate will have a positive potential.
Electric Potential (V) is Electric Potential Energy (U) Normalized for Charge
At this point remember that the Coulomb force is a conservative force, too. So, you can just adopt all the previous steps to the electric field and get a similar definition of electric potential V.
The electric potential is equal to the potential energy of a 1C charge at location r of an electrostatic field.
Similarly to Equations (1-6) you can calculate it from the work done by the electric field (Win) (7, 8) for a charge q=+1C.
Therefore the change in potential between infinity and point r is (substituting (6a) into 8):
These mean:
(7) the electric potential is equal to the “-“ internal work spent by field when “+1C” charge moves from the point with 0-potential energy to the considered space location.
and (8) the change of electric potential between any two space locations is equal to “-“ amount of work done by the field when a charge +1C is shifted between these two locations.
Note: Potential has units of Volts (V), yes the same volts as your car battery!. Using the definition of potential, 1V=1J/C.
When the electric field moves a positive charge along its lines, it does positive internal work. The equation (8) shows that the charge is moved from higher to lower potential because ∆V = V2 -V1< 0. So, if a positive charge is placed inside an electric field, the electric field tends to move it towards locations with lower V-values(2.b). A similar situation is met inside gravitational fields; objects in free fall move towards the earth, decreasing their potential energy. If a negative charge is placed in an electric field the electric force will move it against the field lines. As the electric field does positive internal work
(Wint>0), the equation (8) shows that in this case ∆V = V2-V1 > 0 and V2 > V1. This means that the electric field pushes the negative charges from lower towards higher V values(2.c).

The electric field will push a “+” charge towards lower V-values and a “-“ towards higher V-values.
When a test charge (+1C) is moved by a distance s inside an electric field, the field does work (see 8)
For an infinitesimal displacement ds you get
So, dV E* dsEs * ds(11) and Es dV
And
The equations (11-12) are very important because they relate the two main parameters of the same electric field and show how to calculate one of them if the other one is known.
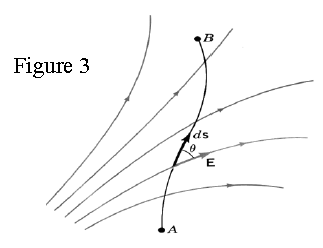
As electric potential is potential energy normalized for charge, its value depends only on the charge's location. So, its change depends only on the initial and final positions and not on the path followed for a shift from “A” to “B”.
This shows how you could calculate the work done by the electric field when a charge is moved inside a non uniform field (fig.3), avoiding complicated integral calculations.
So, for a test charge “+1C” moving inside a non uniform field the work done by the field is calculated as follows:
Better, keep in mind:
Potential and Potential Energy inside a Uniform Field (e.g. inside a Capacitor)
Consider that an external force shifts the positive unit charge (+1C) inside the uniform electric field E from A to B following an irregular path (Fig.4). As we know, the work by electric force ( Fe E ) is
because the field is constant (take out integral) and the
vector sum of infinitesimal shifts is equal to .
As we get
Note that the same result would be for all positions of point B along the direction CB and this means that for all these positions VB = constant. In other words:
The line CB is an equipotential line.

We fix the origin of an axe Ox at point A and select its direction the same as the field. If V=V(0) at origin, then at point B with coordinate x on Ox axis, the eq. (15) is written:
Equation (16) shows us that the potential decreases (Fig.4) while x increases ( E along field sense).
We can conclude that in a uniform field:
a) The potential value is the same on each plane perpendicular to electric field (equipotential planes).
b) The potential decreases while moving along the direction of field; it increases in opposite sense.
c) Dimensional rule applied at (16) gives [V]=[E]*[x] and [V]≡ volt = (N/C)*m= N*m/C=J/C
The equipotential plane is a special case of an equipotential surface “the geometrical place of points with the same potential”. This concept comes from gravitational equipotentials which are depicted as lines in a 2-dimentional plane (see Fig.5). In the case of uniform field we found that:
THE ELECTRIC FIELD LINES ARE PERPENDICULAR TO
THE EQUIPOTENTIALS AND POINT “DOWNHILL” FROM
THE HIGHER TO THE LOWER VALUES OF POTENTIAL.
This is a general rule that applies for all electric fields.
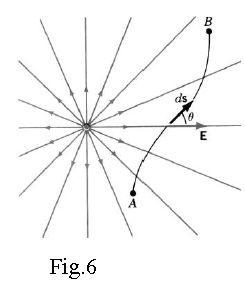
In fact, for a shift ds of test charge along an equipotential line (ΔV = 0),
the work by electric field is zero becauseE* ds Wint V 0
As E* ds 0 means E ds it comes out that the electric field is perpendicular to equipotential line.
Consider a moving charged particle that enters in an electric field. If other forces are negligible, one may apply the energy conservation law for the system field-charged particle. So, if the particle has the kinetic energy K(1) and the potential energy due to the field U(1) at the moment t1, as long as it is inside
the field its total energy will be constant i.e. E = E(1) = K(1) + U(1). This means that ΔE = ΔK+ ΔU = 0
and ΔK = - ΔU . Then, as ΔU = q* ΔV one gets
It turns out that, the kinetic energy of particle may increase or decrease depending on sign of its charge. If q > 0, and the charged particle enters the field moving
a) along the direction of potential decrease (“downhill”), ΔV < 0 and the field will increase its K
b) along the direction potential increase (“uphill”) , ΔV > 0 and the field will decrease its K.
If q < 0, and the charged particle enters the field moving :
a) along the direction of potential decrease (“downhill”), ΔV < 0 and the field will decrease its K
c) along the direction potential increase (“uphill”), ΔV > 0 and the field will increase its K.
These rules are important when dealing with electrons or protons accelerated by use of electrostatic fields. One has introduced a new energy unit “electronvolt (eV) “ which is widely used in chemistry, atomic and nuclear physics. It is the kinetic energy gained by a particle with charge +e when moving downhill through a potential difference of 1V.
The Electric Potential of Point Charges
a) One point charge
The electric field created by a point charge +Q in the space around it is a radial field
We may find the expression for the potential through the work done by
electric force on a charge (+1C) when it moves on a path AB. So,
Note that
By convention, you fix the zero value of potential at ,V(∞) = 0.
Then one gets the potential at point rB ≡ r as
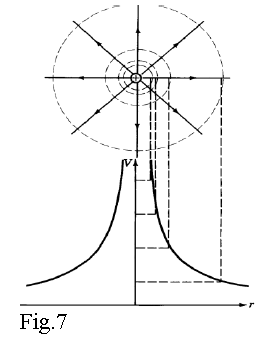
Figure 7 presents graphically this function in 3D space. The dashed circles present the equipotential lines. They are closer to each other near the charge because the potential changes rapidly in this region. The field lines are normal to equipotential lines. Note that the magnitude of field is bigger at locations where the equipotential lines are denser (near the charge which is the source of field) and it decreases at locations where they are rare (big r-values).
b) Two point charges
Consider that two point charges Q1 and Q2 are present at the same space. Let E1_ and E2 be the electric fields corresponding to each of them at a given point of this space. We can find the resultant electric field at this point by applying the superposition principle
As in the case of one particle, we chose the starting point A of a path at infinity (VA= V(∞) = 0) and express the difference of potential through the work done by net electric field during the shift A to B.
In the general case, when the net field is due to several charges Q1,Q2,..Qi the net potential is calculated through the expression
or more generally
Notes: a) ri is the distance from the “ith-charge” to the location “r” where we calculate the potential b) you have to include the charge signs inside the sum (23).
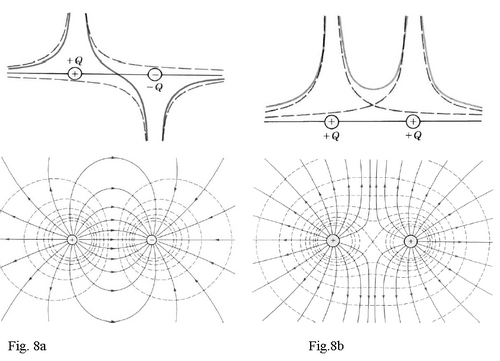
Figure 8.a shows the potential evolution (up) in the electric field built by a dipole and the equipotential lines and the fields’ lines (down). Figure 8.b shows the potential evolution (up) in the electric field due to two equal positive charges, the equipotential lines and the field lines in the plan that contains charges.
Conductors
As explained in section 2.3 the electrostatic field is zero inside a conductor and perpendicular to its surface in the surroundings. As for a path connecting two points located inside
it or on its surface, it turns out that the electric potential of a conductor is the same everywhere on its surface and inside it. Note that this is valid for any charged conductor and any neutral conductor placed inside an electric field.
It is important to know that the presence of a conductor in an external field modifies the field pattern in the close region around its surface so that the field lines become perpendicular to its surface.
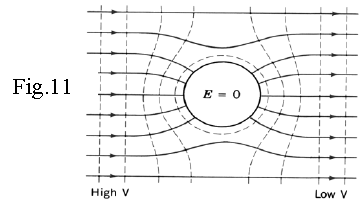
Fig.11 shows the deformation of equipotential surfaces and field lines of a uniform external field around a spherical uncharged conductor. Near the sphere, the equipotential planes become spherical and the field lines become radial.
As the charges are distributed on the conductor surface and the field inside it is zero, one may open a cavity inside the conductor and use the conductor surface as a shield from external fields. This is what happens in a Faraday cage, a device widely used in as a shield against electric fields.
If a conducting wire connects two charged conductor objects, their charge redistributes so that the potential be the same and the field be zero within them and parallel to their surface.
Assume that we place the charge +Q on a metallic sphere. It will be distributed uniformly on the spherical surface and this will bring a constant charge density on the sphere surface. As you may see, the charge density on this surface is bigger for small values of radius R.
This has important implications for all conductors because even when the surface of the metallic object is not spherical, the charge density is always higher at the sharp points (smaller R) and the electric field ( ) is higher at those locations as a consequence.
For this reason, lightning conductors usually end in sharp points to attract the lightning.
This effect can also be used to produce electric fields with very high magnitude. On the other hand, this effect may become problematic because very high E fields can ionize air and may be the origin of corona discharges (=sparking!).
Examples
Example 1: Potential energy of point charges
A positive charge 2.00µC is held on a horizontal plane and a charge of -1µC is held 5.00 cm North of it, and a charge of 3.00µC is held 5.00 cm West of it.
a) What is the total potential energy of the system?
b) What is the potential energy of the 3.00 µC charge?
c) If the 2.00 µC charge is released (let's say the object has a mass equal to 1 gram) what is its speed when it is far far away from the other 2 charges?
Example 2: Potential energy of point charges
A small sphere carrying an unknown charge q1 is held fixed in space. A second small sphere of mass 1 mg carrying charge q2=5.00 µC is projected toward q1.
When q2 is 1.00 m from q1, its kinetic energy is 0.500J.
When q2 is 0.500 m from q1, its kinetic energy is 0.250J.
Does q2 stop and turn around, or does it hit q1?
Example 3: Potential energy of point charges
Charge q1 (-10.0µC) is placed at the origin and charge q2 (1.00µC) is at (3.00,-1.00)cm.
a) What is the electric potential at point P (3.00,2.00)cm?
b) Compare the potential energy of a 10.0 µC charge at point P with that of a -10.0µC charge at point P.
Example 4: Potential energy of point charges
A small object with mass 1.00mg carries extra electrons. When it passes point A, it is moving at 14.15m/s and when it passes point B it is moving at 10.0m/s. Electric forces are the only ones acting on it.
a) Sketch electric field vectors at point A and B, and sketch an electric field line through point C.
b) What is the potential difference between points B and A (= or )?
c) If A is at 25.0V what is the electric potential at B?
Example 5: Drawing equipotential surfaces
A positive charge 2Q is held on a horizontal plane and a negative charge -Q is held left of it.
Sketch the equipotential surfaces around these 2 charges.