Basic Concepts
Kreshnik Angoni
Kinematics is that part of physics that studies the movement itself without paying attention to the reason why it happens. Simply put, it uses one set of physical quantities ( coordinates, velocity and acceleration) to describe how the movement happens without use of forces that cause it.
Dynamics uses the forces to explain why the movement happens. Static uses “the forces” to explain why the object is at rest. In general, the Static is studied in the frame of Dynamics.
ONE DIMENSIONAL KINEMATICS
Introduction
One may distinguish three basic ways of motion: translation, rotation and vibration. Note that in translation and rotation there is no deformation; the object shape and dimensions remain the same. In a vibration motion the object suffers periodic changes in one dimensions or its whole shape.
Translation: All points in the object move in the same way. For each point of the object, the final position can be found by using the same displacement vector (fig.1).

The same displacement vector shifts each object point from position (1) to position (2).
Rotation: The object changes orientation in space. Each object point has a different displacement vector. Even if a rotation is followed by a translation the displacement vectors are different (fig 2.b).

Figure 2.b: Rotation followed by a translation or vice-versa.
Vibration: A periodic change of one dimension or the whole shape.

In figure 3.b, the system (an elastic ball) changes shape (three-dimensions).
Often, in the real life, the three types of movement combine together. We study them separately, by building a physical model for each of them. In this chapter we will deal only with movement along a fixed direction in space (one dimension, 1-D translation).
As mentioned above, in a translation, all object points have the same displacement vector. This simplifies greatly our work; “We study the movement of just one point in the object and the results apply over the object as a whole”. So, one uses a particle motion as a model for the object motion.
Displacement Versus the Traveled Distance
Consider an object (plane, car..) moving along a straight line. We model this motion by a particle in motion along a straight line. To define the position of this particle, we need only one axis. So, we select:
- Frame origin O
- Positive direction
- Length unit "m"
- Time unit "sec"
- t=0 at initial location
Figure 4 presents the 1-D motion of an object. The particle in the model starts its motion at time = 0sec and at position = +1m. It moves 4m right, turns and stops at = -3m. The motion lasts for 2sec.
We define the particle displacement as where is the final location and is the initial location. Note that if the particle is shifted along direction and if it is shifted in opposite direction to axis . Remember: The displacement is not the same as the travelled distance which is always positive. In the case of figure 4, the travelled distance is 4 + 8 = 12m while the displacement is = (-3) - (1) = -4m.

Velocity Versus Speed
How fast is the particle moving? In everyday vocabulary one uses the speed (positive scalar) to answer this question in the case of cars, planes etc. If one does not have specific information about the way the particle is moving in particular portions of its path, one has to refer to the average speed along the path:
average speed = traveled distance / time interval
The average speed along the path is always a positive scalar.
- Example: In the upper mentioned example of 1-D motion, one would find: average speed = 12m / 2sec = 6m/sec.
In physics, one uses the velocity (vector) to describe the way a particle is moving. For 1D motion along Ox one starts by defining the average velocity:
Note that the velocity may be negative or positive.
- Example: In the 1-D motion example, Vav = -4m / 2sec = -2m/sec, which is different from the average speed (6m/sec).
Remember: Although the speed and velocity have the same units (m/s in SI) they are very different.
Note: The displacement and the velocity are both positive when the particle moves along direction.
When the particle moves along opposite direction , they are both negative.
Very often one uses the graph to present the history of a particle motion. The figures 5 & 6 present two such graphs. The average velocity is calculated easily from the slope at these graphs. In the graph of figure 5, it does not depend on initial moment or the length of time interval. The motion follows all time with the same velocity. In the graph of fig. 6, we see that average velocity increases for smaller time interval ( ~ equal, smaller). So, does not offer good information for all situations.

Figure 6: The particle moves at a changing velocity.
Instantaneous Velocity
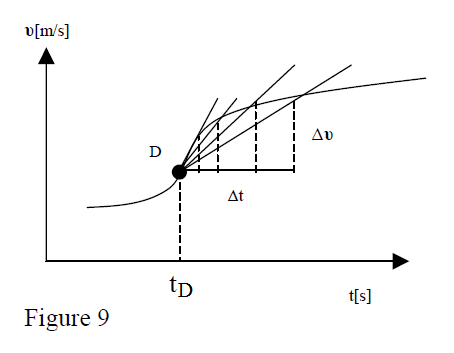
A simple observation of figure 7 shows that for the right information about the particle velocity at point P, one must refer to the smallest time interval counted from the moment when the particle is at point P.

In fact, one may see that the best estimation about the velocity close to point P location is the limiting value of average velocity when the time interval goes to zero. This is the definition of instantaneous velocity at point P:
Note: As this derivative is equal to the slope of curve tangent at point P, one may find the velocity straight from the graph .
The graph in figure 8 presents a motion along axis:

Point B: (larger); Faster motion along
Point C: ; Instantaneous rest, turn back point
Point D: ; Motion along
Point E: (smaller); Slower motion along
Point F: ; Long rest before turning back along
Acceleration
In the popular vocabulary the word “acceleration” means "speed increase". In physics, it means simply a change of velocity vector (magnitude, direction or magnitude & direction simultaneously). Knowing the relation for the motion of a particle, one may build the graph of instantaneous velocity versus time. If it is a straight line, the average acceleration is a constant and is sufficient for the velocity change description. However, such graphs may have different curved parts and one uses instantaneous acceleration.
So, if the average acceleration is defined as
average acceleration = change of velocity / time interval
the instantaneous acceleration at point D is
The acceleration at any point D on the graph is equal to the graph slope at that point. The acceleration may be positive or negative. It is important to mention that the acceleration sign alone is not sufficient to understand whether the particle is speeding up or slowing down. To get this information, one must compare the sign to the sign. The following table describes all four possible situations.
| is POSITIVE | is NEGATIVE | |
|---|---|---|
| is POSITIVE | Velocity and acceleration have the same sign so the body is speeding up. Velocity is positive which means the motion is along . | Velocity and acceleration have opposite signs so the body is slowing down. Velocity is negative which means the motion is along . |
| is NEGATIVE | Velocity and acceleration have opposite signs so the body is slowing down. Velocity is positive which means the motion is along . | Velocity and acceleration have the same sign so the body is speeding up. Velocity is negative which means the motion is along . |
Remember: The direction of motion is always shown by the sign of velocity.
To get a better meaning of this, let's consider the and graphs in figure 10:

A-point: ; motion along
Since (opposite sign), there is "slowing down"
Between A & B: = max, (slope on ) = max; there is "slowing down"
B-point: , but ; this means instantaneous rest
Since , ready to move along
Between B & C: , ; motion along
C-point: max acceleration
Between C & E: ; motion along
Since but decreasing, slight increase
I-point: zero acceleration; instantaneous constant velocity
Between I & J: ; motion along
Since , there is "slowing down"
Between G & H: greater "slowing down" effect
Beyond G-point: the stopping effect decreases until it becomes zero at point J (constant velocity)
Notes: In real life the velocity cannot change instantaneously. This means that the acceleration has always a finite value (no infinite). At this level, we will study only motions with constant acceleration. To describe a 1-D motion with constant acceleration only ", , and " parameters are needed.
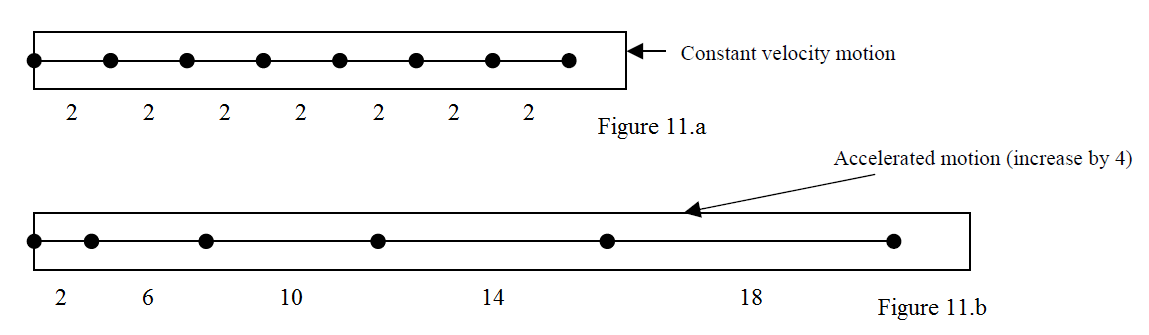
A simple way to distinguish an accelerated motion () from one with constant velocity (): Fix an interval of time (say 1sec) and measure the travelled distance for several successive intervals of 1 second. If the distances are equal, there is a motion with constant velocity (fig 11.a). If the successive distances increase (or decrease) by the same quantity, there is a motion with constant acceleration (fig 11.b). If the successive distances change differently, there is a change of acceleration.