Conservation of Energy EX 4

The block falls losing gravitational potential energy and gaining kinetic energy. It hits the top of the spring and compresses it some distance $x$, losing kinetic energy while the spring gains potential energy. The compression stops when the mass-spring system no longer has any kinetic energy. In this process the block moves down the vertical distance $0.6+x$.

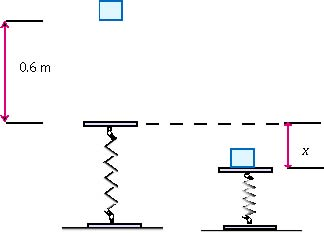
The change in gravitational potential energy of the system Earth-block-spring is negative because the block moves down spontaneously and can be computed as follows:

$U_G=-mgh=-(0.5)(10)(0.6+x)$

The system gained the potential energy of the spring because the initial compression of the spring is $x_i=0$ and the final compression of the spring is $x_f=x$. We can compute the change of the spring potential energy as follows:

$\mathrm{\Delta }{U}_{sp}=\frac{1}{2}k{x_f}^2-\frac{1}{2}k{x_i}^2=\frac{1}{2}k{x}^2$

The block is initially at rest and stops when the spring is at maximum compression and therefore both, the initial and final kinetic energy is zero. The change of the kinetic energy is also zero ($\mathrm{\Delta }K=0$).

There are no non-conservative forces acting in this system or on this system and therefore, the change of the mechanical energy is also zero ($\mathrm{\Delta }E=0$). Given that

$\mathrm{\Delta }E=0$

$\mathrm{\Delta }K+\mathrm{\Delta }{U}_G+\mathrm{\Delta }{U}_{sp}=0$

$0+[-(0.5)(10)(0.6+x)]+[\frac{1}{2}(120)x^2]=0$

$-3-5x+60x^2=0$

We have substituted in the above equation the expression for $\mathrm{\Delta }K$, $\mathrm{\Delta }{U}_G$ and $\mathrm{\Delta }{U}_{sp}$ and obtained a quadratic equation.

Solving the quadratic equation for $x$, we obtain

$x=0.266m$

Note that $x$ is a distance and therefore, it is positive. the positive solution was chosen.