Conservation of Energy EX 5

(a) The diagram below shows the system of mass $m_{1} = 5$ kg, $m_{2} = 3$ kg and the massless spring ( $k = 32$ N/m) at the beginning and when it reaches the maximum displacement.

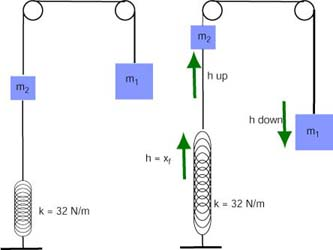
The system starts at rest and therefore its initial kinetic energy is zero. The larger mass falls down pulling the smaller mass up and extending the spring. The force of the spring opposes the fall and so the system will come to rest before it bounces back. This is the moment when the spring reaches its maximum extension and the blocks reach their maximum displacement. This implies that the kinetic energy of the system is zero and consequently, the change in kinetic energy is zero ( $Δ K = 0$ ).

The spring is initially unextended, so $x_{i} = 0$ . Once the mass $m_{2}$ falls the height $h$ , the spring is extended by $x_{f} = h$ . The change in potential energy of the spring is $Δ U_{s p} = \frac{1}{2} k {x_{f}}^{2} - {\frac{k}{x_{i}}}^{2} = \frac{1}{2} (32) h^{2} - 0 = 16 h^{2}$ .

Both masses change their heights and therefore the total change in gravitational potential energy is the sum of $Δ U_{1}$ (the change in gravitational potential energy of $m_{1}$ ) and $Δ U_{2}$ (the change in gravitational potential energy of $m_{2}$ ). $m_{1}$ moves down by height $h$ and so $Δ U_{1} = - m_{1} g h = - (5) (10) h = - 50 h$ . $m_{2}$ moves up the height $h$ and so $Δ U_{2} = m_{2} g h = (3) (10) h = 30 h$ . The total change in gravitational potential energy is $Δ U_{G} = - 50 h + 30 h = - 20 h$ .

The work done by non-conservative forces is zero.

By substituting into the law of conservation of energy $Δ K + Δ U_{G} + Δ U_{s p} = W_{N C}$ we get:

$0 + (- 20 h) + 16 h^{2} = 0$

By dividing the equation by $h$ and isolating $h$ on the left-hand side, we get

 $h = 1.25 m$

(b) The blocks stopped when the block $m_{2}$ fell 1.25 m. It means that the block was still moving when it only fell 1 m. Therefore, at this moment the $K_{f}$ is not zero. We can write:

$Δ K = K_{f} - 0 = K_{f}$

The change of the potential energy of the spring at this moment is:

$Δ U_{s p} = 16 h^{2} = 16 (1)^{2} = 16 J$

The total change of gravitational potential energy of the system is $Δ U_{G} = - 20 h = - 20 J$ . By substituting again into the equation for the conservation of energy we get:

$K_{f} + (- 20) + 16 = 0$

From this equation we get that the final kinetic energy is 4 J. The total moving mass is 8 kg and therefore the speed is

 $v = 1 m / s$

Conservation of Energy EX 5

Navigation menu

Search