Equations of Motion

Helena Dedic

Derivation of Equations of Motion

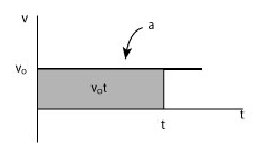
Consider a v-t graph for an object moving with constant velocity.

• Motion with constant velocity implies that the acceleration is equal to zero and therefore the v - t graph is a horizontal line.

$v(t)=v_{o}$

• The displacement is the area under the v - t graph

We write $\Delta x(t)=v_{o}t$

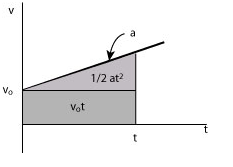
• Motion with constant acceleration implies that the velocity is a linear function of time. Given that the initial velocity is $v_{0}$ we can write

$v(t)=v_{o}+at$

where the acceleration is the slope of the graph and$v_{o}$ is the intercept.

• The displacement is the area under the v - t graph

We write

$\Delta x(t)=v_{o}t+{\frac {1}{2}}at^{2}$
 

• The displacement in both cases is $\Delta x(t)=x(t)-x_{o}$

• There are two independent equations describing motion with constant acceleration and five variables: $\Delta x(t)$, v(t), $v_{0}$, a and t. Consequently, in any problem we can solve for two of those variables and three other must be given.

• We can derive another useful equation by eliminating t from the two equations above.

We begin with equation

$v(t)=v_{o}+at$

We isolate t:

$t={\frac {v(t)-v_{o}}{a}}$ 

Then we substitute for t in the equation for the displacement:

$\Delta x(t)=v_{o}\left({\frac {v(t)-v_{o}}{a}}\right)+{\frac {1}{2}}a\left({\frac {v(t)-v_{o}}{a}}\right)^{2}$ 
 

We will now multiply both sides by 2a. This step will eliminate fractions from this equation.

$2a\Delta x(t)=2av_{o}\left({\frac {v(t)-v_{o}}{a}}\right)+2a{\frac {1}{2}}a\left({\frac {v(t)-v_{o}}{a}}\right)^{2}$ 
 

This leads to:

$2a\Delta x(t)=2v_{o}(v(t)-v_{o})+(v(t)-v_{o})^{2}$ 
  

Expanding:

$2a\Delta x(t)=2v_{o}v(t)-2v_{o}^{2}+v^{2}(t)+v_{o}^{2}-2v_{o}v(t)$ 
  

which leads to:

$2a\Delta x(t)=-v_{o}^{2}+v^{2}(t)$ 
  

This can finally be written in the form:

$v^{2}(t)=v_{o}^{2}+2a\Delta x(t)$ 

Exercises

• Problem solving using equations of motion

Free Fall

• Free Fall

Projectile Motion

• Projectile Motion