Exercises on Vectors
Vector Addition
Helena Dedic
Ex 1
Three vectors are specified as follows: A is 5 m at N of E, B is 7 m at E of S, and C is 4 m at W of S. Find the magnitude and direction of their sum.
Solution
We start by drawing a diagram that shows each vector with its tail at the origin and then by computing the angle with x-axis.
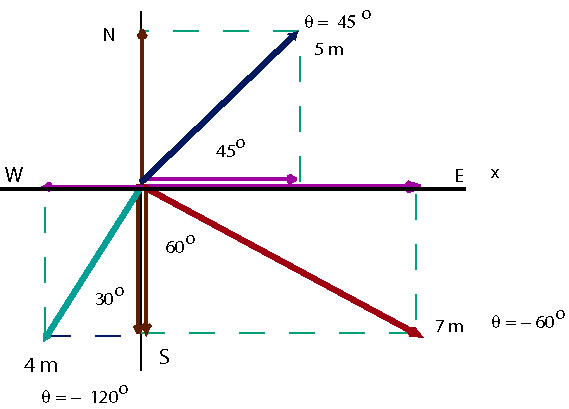
We calculate the value of each component.
We then compute the magnitude and the direction of R:
Ex 2
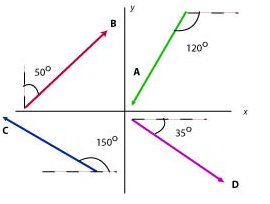
Four vectors, each of magnitude 2 m, are shown in the figure.
a. Express each in unit vector notation. b. Express their sum in unit vector notation. c. What is the magnitude and direction of their sum?
Solution
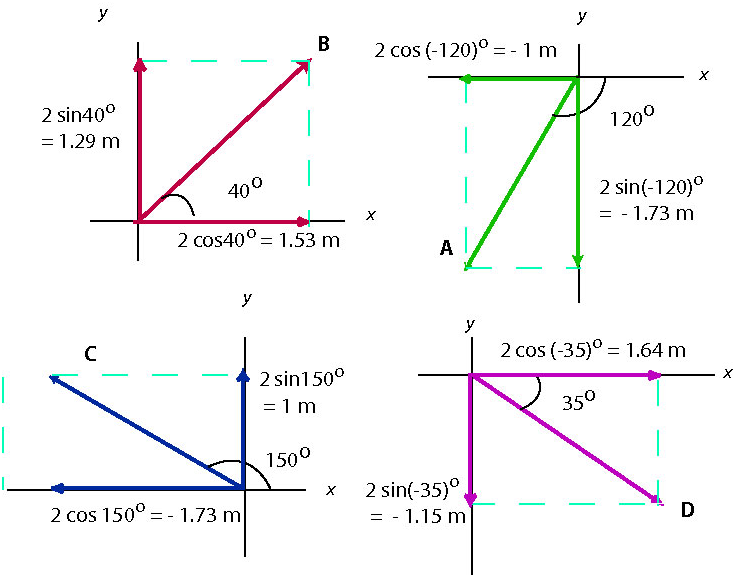
a) We start by placing the tail of each vector at the origin of rectangular coordinates and finding the x- and y-components of each vector:
m m m m
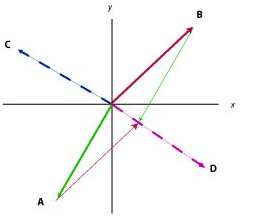
b) We can predict the sum A+ B + C + D by doing a rough sketch, adding the vectors graphically. C and D roughly cancel and we can predict that the sum of A and B is in the fourth quadrant.
We add the vectors by adding x- and y-components
The sum, as predicted, is in the fourth quadrant.
c) We find that the vector sum has the magnitude 0.73 m and it points below the x-axis.
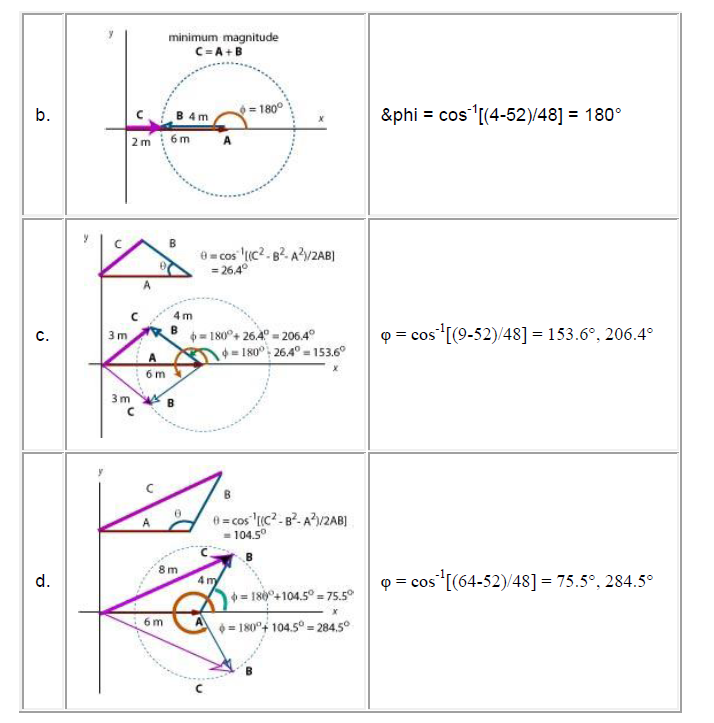
Ex 3
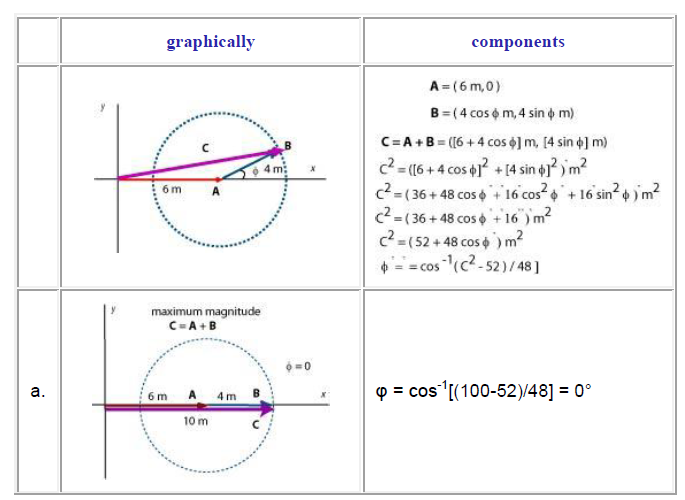
The vector A has a magnitude of 6 m and vector B has a magnitude of 4 m. What is the angle between them if the magnitude of their resultant is:
a. the maximum possible b. the minimum possible c. 3 m d. 8 m
Do each part graphically and by components. (Let A lie along the x-axis.)
Solution
Ex 4
The displacement A is 6 m east. Find displacement B if the magnitude of A - B is half that of A and points in the direction N of E.
Solution
We define C = A - B
Solving for B:
B = A - C
We know that C = 3 m and its directions as measured from the positive x-axis is . We can compute the components of C as follows:
Given that and we compute the components of B