Inertia
Kreshnik Angoni
INERTIA AND THE FIRST LAW OF NEWTON
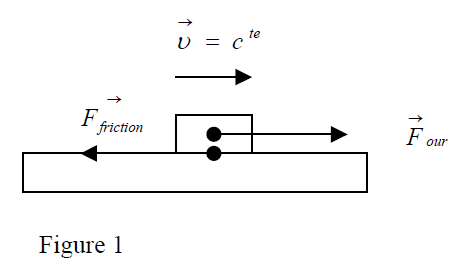
Everyday, experience tells us that "if one does not push a moving body, it will slow down until it is at rest," because "the resting state is the natural state of objects." But here, we are forgetting an action: the friction with the surrounding medium (e.g.: friction of a wooden block with the table on which it is moving.) What if the friction could be avoided? By using oil, the block would follow its road a for much longer.
Galileo's abstraction: What if there was no friction at all = zero external action on the body? Answer: The block would follow its way with constant velocity without slowing down at all = "Galileo’s principle of inertia". He was the first to use the word "inertia = property of an object to keep moving with constant velocity if no force is exerted on it".
- Drop carefully and vertically a block on a horizontal table. There will be no motion even if there is oil on table. The block will stay at rest on table unless a horizontal force pushes it. So, if it is initially at rest, the object will follow to be at rest as long as "the net force exerted on it is zero."
By combining this observation with Galileo's principle, Newton formulated his first law of mechanics:
- A more precise qualitative definition for inertia, related to the body itself, appeared with time:
To get the quantitative definition of inertia we will refer to the second law of Newton. For now remember that:
a) The first law works when there is zero net force acting on the body.
Ex.: We push an object so that it moves on a table with constant velocity. This means that the sum of our force and friction force is equal to zero.
b) The inertia opposes any change in velocity (not only in magnitude but in direction too.)
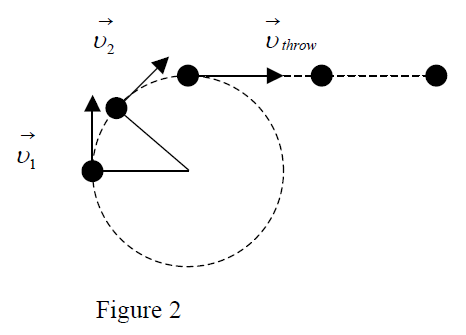
Ex.: In discus throwing (sport), the sportsman's arm forces the disk to change the direction of its velocity. The sportsman feels the inertia opposition on his arm. When he lets go, the discus continues in a straight line along the direction of instantaneous velocity (due to inertia.)
RELATED VIDEOCLIPS
INERTIAL REFERENCE FRAMES
The first step in a physics study is the selection of a coordinate system - the axis orientations by unit vectors - but, how to fix the origin? The origin is fixed on an object that is called the reference frame. Next, when we study a particle motion, we deal with a "motion with respect to this reference frame."
Ex.: A man walking at 5 km/h in a train moving at 50 km/h with respect to the station. If we tie the origin to the station (earth), the results concern the man's motion with respect to the station (reference frame = station or earth). If the man walks in the same direction as the train's movement versus earth, his velocity is 55 km/h (versus earth). If we tie the origin to the train (reference frame), the results concern his motion with respect to the train. In this case, the man’s velocity is 5 km/h (different from 55 km/h.)
A very long transparent wagon with frictionless floor moving at a constant velocity of 50 km/h versus the station. Two observers, O, seated at the station, and O', seated in the wagon, observe a ball inside the wagon.
a) The ball is at rest in the wagon. For the observer O', the ball will be at rest for all time (unless someone gives it a kick) because the ball keeps its state of motion of being at rest versus the wagon. The observer O sees the ball moving for all time with constant velocity 50 km/h. For O, too, the ball keeps its state of motion (moving at 50 km/h versus the station for all time.)
b) The ball is moving at 5 km/h versus the wagon in the same direction as the train's motion versus the earth. For the observer O', the ball will move at 5 km/h for all time because the ball keeps its state of motion of 5 km/h versus the wagon. The observer O sees the ball moving for all time with constant velocity 55 km/h. For O, too, the ball keeps its state of motion (moving at 55 km/h versus the station for all time.)
So, the first Newton's law is equally applied for observers O and O' in these two frames.
Two important conclusions derived from our "experiment":
- In an inertial frame, if the net force applied on an object is zero, the object will remain in its state of motion: either at rest or moving at a constant velocity.
- If a frame is verified to be inertial, any other frame that is at rest or moving at constant velocity versus , is also an inertial frame.
Let the ball be at rest in the train. Consider now that the wagon accelerates its movement (versus earth). As the floor is frictionless, it cannot take the ball with it (exerts no force upon the ball) while moving with acceleration; the floor will slip under the ball. The observer O' (who moves with acceleration and feels it due to the seat's action on his back) will see the ball starting to move backward. He will say, "The ball does not keep its state of motion even though there is no force action on it" because, for him, the ball was at rest and starts moving. So, the first Newton's law does not apply.
At the same time, the observer O sees the ball following to move in the same way (at constant velocity 50 km/h). So, for him, the first Newton's law applies. This experiment shows that if we have a verified inertial frame and another frame moving with acceleration versus , the frame is not an inertial frame. The second frame is called a noninertial frame. The motion of bodies with respect to such frames does not obey to first Newton’s law.
How do we decide whether a frame is inertial or not? We proceed by experiments. Such experiments show that the first law of Newton applies on the earth's surface. So, one considers the earth as an inertial frame. Therefore, any frame at rest with respect to earth (building, room, table, mountain, tree, etc.) or moving with constant velocity versus the earth (train, plane, car, etc.) is equally a inertial system for experiments done on the earth's surface. Note that from this point of view there is an infinite amount of inertial frames.
The assertion that "the earth is an inertial frame" is based on lab experiments. So, it is proved true for "small areas over the earth, like labs." An experiment in a bigger scale proves that, the earth is not "a perfect inertial frame." Let’s explain why. Consider a ball moving with constant velocity in the North-South direction over a frictionless plane (figure 3).
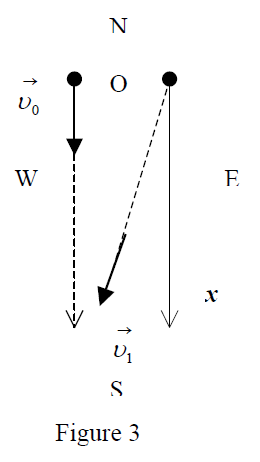
To verify the inertia law, one observer at rest ties the origin to his position on the earth, draws the axis along the direction N-S and checks the direction of velocity vector. As the earth rotates in direction W vs E, the straight line shifts versus E and the ball "find itself on the West of the reference line." For the observer (earth frame), the velocity has changed direction. So, the ball "is not keeping the same state of motion with constant velocity. This means that the reference frame (earth) is not an inertial frame."
Note that the daily rotation is quite slow: there is one turn per day, which means a rotation of 360/(24*60*60) = 0.00416 degree per second: this is why we cannot feel it. However, if we would observe the motion over many minutes (say 10min), the effect would be visible (10*60*0.00416 = 2.5 degrees). So, one would say that the earth is not a real inertial frame, but it is a very good approximation for the majority of experiments performed its earth surface.
For the interplanetary studies, a frame with origin on the sun is a very good approximation of an inertial frame. For the time being, no 100% real inertial frame has been found, yet...
MORE VIDEOCLIPS
Understanding Inertial and Non-Inertial Frames