Introduction to 2 D Motion
Helena Dedic
• When a path of a particle is a straight line we say that its motion is one dimensional. In such cases we orient one of the axis along the path traveled by the particle and we can describe its position or velocity by one of the components - see two examples below:
• When a path of a particle is a curve in a plane (let say horizontal plane or vertical plane) then we say that its motion is a two dimensional motion.
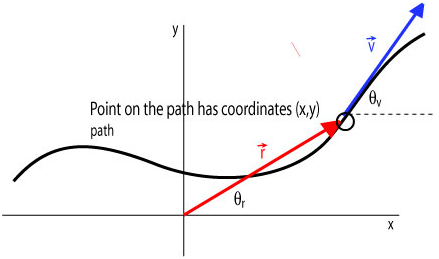
• The position vector at any instant t has two components each of which is a function of time.
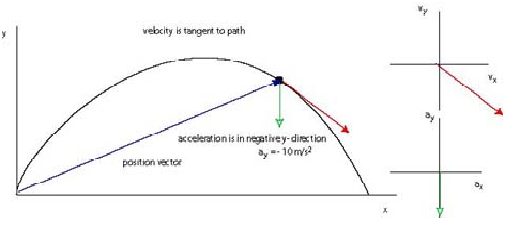
• The velocity vector points in the direction of the tangent to the path. We cannot deduce its magnitude but we know that it has two components neither of which is zero at t
• The acceleration vector also has two components. We cannot deduce either the direction or its magnitude from the diagram above.
We will study two cases of two-dimensional motion: projectile motion and motion with constant acceleration.
Exercises
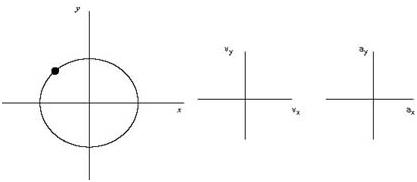
Sketch the displacement, velocity and acceleration vectors when the particle is in the position shown:
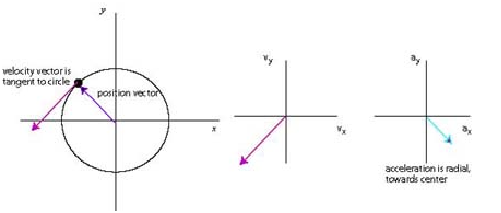
a. A particle moves counterclockwise in a circle.
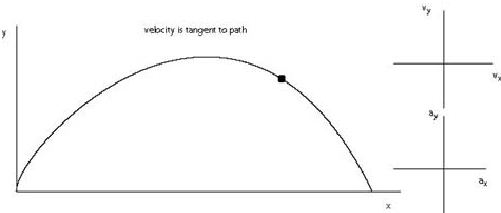
b. The path of a projectile is given below.
a. The position vector is a vector that points from the origin of the coordinate system to a point where the particle is located. See the diagram below.
The vector of velocity is a tangent to the path of the particle and points in the direction of motion. In this case, the particle moves counterclockwise and so we drew the arrow as showm below. The acceleration of the circular motion always points towards the centre of the circle (path) and so we drew the vector pointing along y-axis.
b. The position vector is a vector that points from the origin of the coordinate system to a point where the particle is located. See the diagram below. Note tnat the drawing seems to indicate that the particle movesd from the origin (initial position) to the point indicated in the diagram. Consequently, the position vector and the displacement vector from the beginning of the motion are equal.
The vector of velocity is tangent to the path of the particle and points in the direction of motion. At this point the projectile is still rising up and so the velocity vector points above the horizontal axis. On the other hand, the acceleration always points down and therefore the components of the acceleration in the chosen coordinate system are