Newtons Laws EX 19

(a) $a=4m/s^2$

There are three forces acting on mass $m_2$: $F_G$, $F_N$ (contact with the horizontal surface) and $F_T$ (contact with the massless rope). The forces acting on the mass $m_1$ are: $F_G$ and $F_T$ (contact with the massless rope). We note there is no other object in contact with $m_1$ and therefore no other force. We also note that the tension in the rope is the same at both ends of the rope since the pulley and the rope are massless. The diagram below shows the forces and the acceleration of the system:

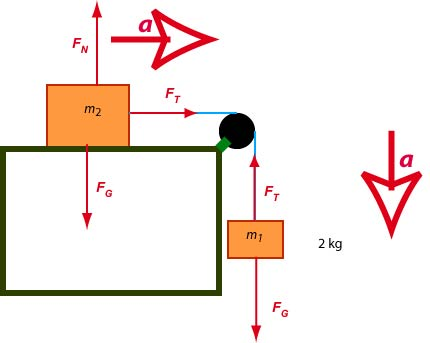
We choose the coordinate system for each of the blocks so that the x-axis points to the right (the acceleration is positive) for $m_2$ and the x-axis pointing down (the acceleration is positive as well) for $m_1$.

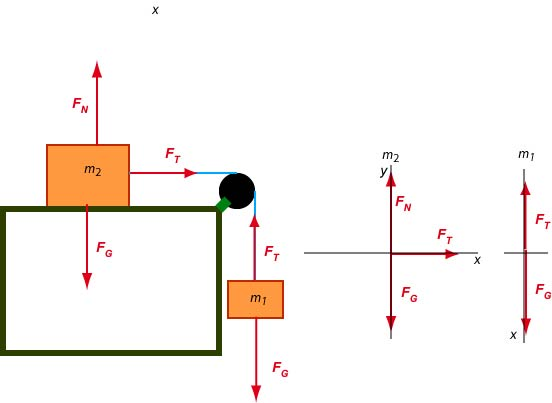
Now we will compute the components of all forces for each block:

	$m_1$	$m_2$
	x-axis	x-axis	y-axis
$F_G$	20 N	0	$-m_{2}g$
$F_T$	$-F_T$	$F_T$	0
$F_N$		0	$F_N$

Now we can write the equations for Newton's Second Law for both masses:

$20-F_T=m_{1}a=(2kg)(4m/s^2)=8N$


$F_T=m_{2}a=4m_2$


$F_N-m_{2}g=0$

Our task is to determine $m_2$ so we will solve for $F_T$ from the first equation finding $F_T=12$ N. We will then replace this value in the second equation and find $m_2=3$ kg.

(b) Now we will use the same system of axis and determine for what value of $m_2$ is the tension equal to 8 N. The components will now have these values:

	$m_1$	$m_2$
	x-axis	x-axis	y-axis
$F_G$	20 N	0	$-m_{2}g$
$F_T$	-8 N	8 N	0
$F_N$		0	$F_N$

Now we can write the equations for Newton's Second Law for both masses:

$20-8=m_{1}a=2a$


$8=m_{2}a$


$F_N-m_{2}g=0$

Our task is to determine $m_2$ so we will solve for $a$ from the first equation finding $a=6m/s^2$. We will then replace this value in the second equation and find $m_2=1.33$ kg.