Newtons Laws EX 22

We draw all the forces acting on the plane and its free-body diagram. A force due to the air pressure under the wings lifts the plane and allows it to fly. This force is is perpendicular to the wings. A pilot sitting in the cockpit experiences the gravitational force and a normal force exerted by the seat which also perpendicular to the wings. From the picture we gather that the center of the horizontal circular path of the plane is on the left of the plane and so the centripetal acceleration points to the left. We choose the horizontal x-axis and draw the free body diagram.

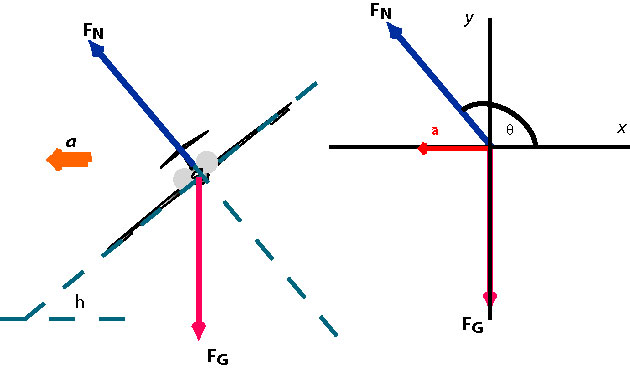
(a) Since the plane travels with velocity $v$ in a circle of radius $r$, the magnitude of the acceleration $a$ is equal to ${v^{2} \over r}=1.54m/s^{2}$. The acceleration points in the negative direction and so its horizontal component is negative.

Now we compute the components of the forces:

Forces	x-component	y-component
$F_{N}$	$F_{N}\cos(\theta )$	$F_{N}\sin(\theta )$
$F_{G}$	0	-700 N
$\Sigma F$	70(-1.54) N	0

Now we write the equation:

$F_{N}\cos(\theta )=70\times -1.54=-107.8N$
$F_{N}\sin(\theta )-700=0$

First, we rewrite the second equation as $F_{N}\sin(\theta )=700N$. Solving this system of equations to find the angle requires us to divide this last equation by the equation we obtained for the x-component. In this step, we eliminate the magnitude of the normal force from the equation.

${F_{N}\sin(\theta ) \over F_{N}\cos(\theta )}={700 \over -107.8}=-6.49$

${\sin(\theta ) \over \cos(\theta )}=-6.49$

$\tan(\theta )=-6.49$

$\theta =-81^{\circ }+180^{\circ }=99^{\circ }$

Note that we need to add 180° because the x-component of the force is negative. We have found the angle that the normal force makes with the horizontal axis. Since the wings are perpendicular to the normal force, the wings make an angle of 9° with the horizontal axis.

(b) Now we are ready to compute the magnitude of the normal force.

$F_{N}\sin(99^{\circ })=700$

$F_{N}={700 \over \sin(99^{\circ })}=708N$