Newtons Laws EX 32

A car traveling at 100 km/h needs a distance of 60 m to stop. We are asked to determine the stopping distance on an uphill slope.

First, it is important to note that we need to assume that the car skids to a stop. Thus, the force of kinetic friction causes the car to decelerate. Since the character of the surface is unchanged, the coefficient of kinetic friction remains the same both on the flat surface and on the uphill surface.

The problem is that we are not given data to solve the uphill stopping distance: we don't know the coefficient of friction nor the mass of the car and thus we cannot find the net force and then the acceleration of the car. The only data we have available is the information about the flat surface stopping distance. We have to attempt to use this data to "fill in the blanks" in the uphill case. We will assume that the car has mass $m$ and proceed with the calculation as if it were a known value. This is a good problem solving technique that you should remember. If it appears to you that you are missing some data (like the mass of the car) assign to it a symbolic value (like $m$) and proceed with your solution. It will often happen that $m$ is "cancelled out" in the course of your calculations.

Now proceed to use the data from the travels on the flat road. The velocity changes from $v_{i}$ = 100 km/h = 27.7 m/s to $v_{f}$ = 0 while the displacement is 60 m. From this information we can determine the acceleration $a$ using the following equation of kinematics:

${v_{f}}^{2}={v_{i}}^{2}+2a\Delta x$

In our case,

$0=(27.7)^{2}+2a(60)$

so that solving for a gives $a=-6.39m/s^{2}$. Note that, in this case, the direction of the acceleration is opposite to the velocity. Knowing acceleration, we can determine the other forces acting on the car. In particular, we can determine the magnitude of the frictional force, from which we can determine the coefficient of kinetic friction. Since the surface remains unchanged, the coefficient of kinetic friction along the hill is the same as that along the flat road.

Finding the coefficient of friction:

The car is the system, its mass is $m$.

The forces acting on the car are $F_{G}$, $F_{N}$, $F_{f}$.

Acceleration is opposite to the velocity: $a=-6.39m/s^{2}$. We choose the coordinate system with the x-axis parallel to the road. The diagram below shows the forces and the associated free body diagram.

The components of these forces are:

Forces	x-component	y-component
$F_{G}$	0	-m g
$F_{N}$	0	$F_{N}$
$F_{f}$	$-F_{f}$	0

Note that we will used $g=10m/s^{2}$.

We write the equation for the y-component and find that

$F_{N}=mg$

Substituting into the equation for kinetic friction, we get that

$F_{f}=\mu _{K}F_{N}=\mu _{K}mg$

And writing the equation for the x-component

$-\mu _{K}mg=ma$

we get that

$\mu _{K}={-a \over g}={-(-6.39) \over 10}=0.639$

1. Moving up a 10º incline

Now we will find the acceleration along the incline using the same method as above.

The car is the system, its mass is $m$.

The forces acting on the car are still $F_{G}$, $F_{N}$, $F_{f}$.

The acceleration is opposite to the velocity and we will again choose the coordinate system so that the x-axis is parallel to the road. The diagram below shows these forces and the associated free body diagram.

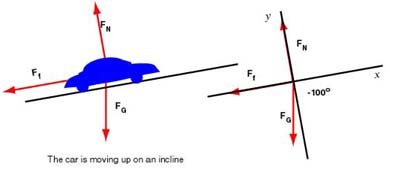
The diagram shows the angle for the weight, and we compute its components as follows:

Forces	x-component	y-component
$F_{G}$	$mg\cos(-100^{\circ })=-1.73m$	$mg\sin(-100^{\circ })=-9.85m$
$F_{N}$	0	$F_{N}$
$F_{f}$	$-F_{f}$	0

From the equation for the y-component we find that

$F_{N}=9.85m$

The force of kinetic friction is therefore

$F_{f}=\mu _{K}F_{N}=(0.639)(9.85m)=6.29m$

The equation for the x-component is:

$-6.29m-1.73m=ma$

Solving for $a$, we find $a=-8.02m/s^{2}$

Knowing the acceleration, we find the stopping distance $\Delta x$ using the kinematic equation

$0=(27.7)^{2}+2(-8.02)\Delta x$

and solving gives $\Delta x=48$ m.

2. Moving down a 10º incline

We solve for stopping distance in much the same way. We list the forces and draw the free body diagram:

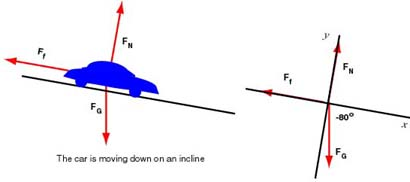
The diagram shows the angle of the weight. We compute its components as follows:

Forces	x-component	y-component
$F_{G}$	$mg\cos(-80^{\circ })=1.74m$	$mg\sin(-80^{\circ })=-9.96m$
$F_{N}$	0	$F_{N}$
$F_{f}$	$-F_{f}$	0

From the equation for the y-component we find that

$F_{N}=9.96m$

Then the force of kinetic friction is

$F_{f}=\mu _{K}F_{N}=(0.639)(9.96m)=6.36m$

Now we will write the equation for the x-component:

$-6.36m+1.74m=ma$

Solving for $a$, we find $a=-4.62m/s^{2}$

Knowing acceleration, we find the stopping distance $\Delta x$ using the kinematic equation:

$0=(27.7)^{2}+2(-4.62)\Delta x$

Solving for $\Delta x$, we find $\Delta x=83$ m.