Newtons Laws EX 5
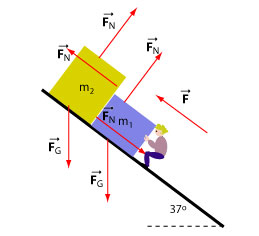
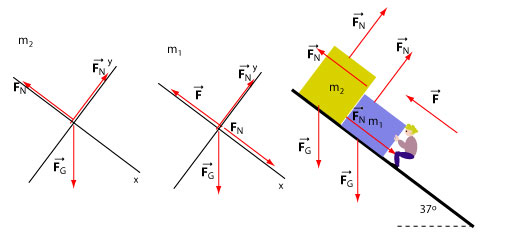
Firstly, we focus on the blue box of mass kg. The box is in contact with the surface of the incline and the surface of the box . Therefore, there are two normal forces: which is exerted by the incline and which is exerted by the box on the box . In addition, there is a gravitational force and the force that is exerted by Sally on . Secondly, we list the forces exerted on the yellow box of mass kg. This box is in contact with the surface of the incline and the surface of the box . Therefore, there is the normal forces exerted on this box by the incline and the normal force exerted by the box . In addition, there is also the gravitational force exerted on it. It is important to note that the force is exerted by Sally only on the blue box . Sally is not in contact with the yellow box and therefore she does not exert any force on it.
The blocks are at rest and therefore the sum of the forces on each box is zero. To draw a free body diagram for each of the boxes we select the x-axis parallel to the incline.
To determine the components of forces, we will begin with forces exerted on the blue box. The gravitational force makes and angle of -53° with the positive x-axis.
| Forces | x-component | y-component |
|---|---|---|
| 180 cos(-53°) = 108 N | 180 sin(-53°) = -143 N | |
| 0 | ||
| 0 | ||
| 0 |
Note that we used in our calculations.
We deal first with the y-component:
This yields N
Now we write the equation for the x-component:
We cannot solve this equation. First, we need to consider the yellow box.
The forces exerted on are , the normal force exerted by the blue box and the normal force exerted by the incline . The gravitational force makes the angle of -53° with the positive x-axis.
The components of the forces exerted on are:
| Forces | x-component | y-component |
|---|---|---|
| 250 cos(-53°) = 150 N | 250 sin(-53°) = -200 N | |
| 0 | ||
| 0 |
We write the equation for the y-component:
This gives us N.
The equation for the x-component yields:
We have two equations with two unknowns:
By adding the two equations we solve N.
We solve the second equation for N.