Newtons Laws EX 8

First we have to picture this problem.

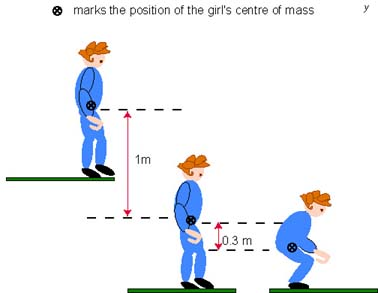
As she steps of the ledge she will be falling freely until her feet touch the floor. In the question a) her torso will continue to move down 30 cm - see the diagram below.

Before her feet touch the floor the only force exerted on her body is the gravitational force of 400 N (no contact).

When her feet touch the floor the two forces act on her body: the gravitational force of 400 N and the normal force $F_{N}$.
The question a) refers to "force exerted on her torso". Since the statement is not clear we may interpret it simply as the net force exerted on the torso while it slows down. In this case we need determine the acceleration and find $F_{net}=ma$.

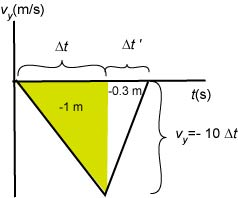
We can use what we learned in kinematics to find the acceleration. The child is at rest on the ledge and gains speed at a rate of 10 m/s/s while her center of mass moves down - 1 m. Then she comes to rest while her center of mass still moves down - 0.3 m. The v - t graph looks like this:

In this graph we can determine the interval of time while the girl falls down 1 m as follows -1 = ½ (-10 $\Delta t$)$\Delta t$. Solving for $\Delta t$ we find $\Delta t=0.45$s. The downward velocity just before the girl touches the ground is $v_{y}=-10\Delta t=-10*0.45=-4.5$m/s.

Then she slows down and comes to stop while she is still moving down - 0.3 m. The acceleration is positive in this situation (the acceleration is opposite to her velocity). Note that her acceleration varies during this motion but we will determine the average acceleration by drawing a straight secant line. From the area under the graph we find how long does it take to come to rest:

$-0.3={\frac {1}{2}}(-4.5)\Delta {t'}$.

We find $\Delta {t'}={\frac {0.6}{4.5}}=0.13$s. The average acceleration is then $a=(0-(-4.5))/0.13=33.3m/s^{2}$.

The average net force is then $F_{net}=40*(33.3)=1333N$. The positive sign indicates that the force points upward.

Similarly, for question b: the displacement while the girl is bending is - 0.04 m. From the area under the curve we find how long does it take to come to rest:

$-0.04={\frac {1}{2}}(-4.5)\Delta t'$.

We find $\Delta t'=0.08/4.5=0.018s$.

The acceleration is then $a=(0-(-4.5))/0.018=250m/s^{2}$.

The net force is the $F_{net}=40*250=10000N$. The positive sign indicates that the force points upward.

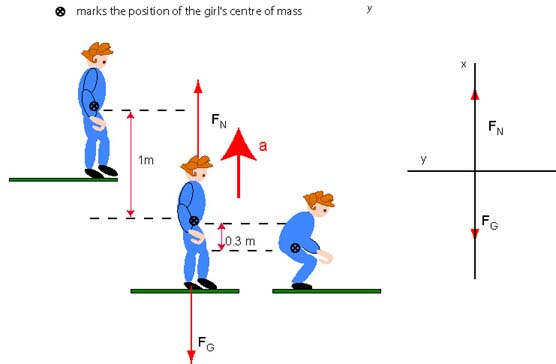
As we said above we may interpret this problem by assuming that we are to determine the net force on the child. In such case we solved the problem. Another possibility is to assume that the question requires us to think about the normal force exerted on the child's feet. When her feet are in contact with the floor, there are two forces acting on her $F_{N}$ and $F_{G}$. Her acceleration points upward and therefore we point the x-axis upward as shown below:

Given that y-components of both forces are equal to zero we can write the equation for x-components.

In question a.: $F_{N}-400=1333$. Solving for $F_{N}$ we find $F_{N}=1733N$

In question b.:$F_{N}-400=10000$. Solving for $F_{N}$ we find $F_{N}=10400N$.

This example shows how important it to flex your knees! You need to minimize the force exerted on the bones of your body.