Proj Motion EX 4

Helena Dedic

A rocket launched from rest at $70^{\circ }$ to the horizontal has a constant net acceleration of 8 m/s2 along this direction for 6.5 s and then is in free fall. Find its maximum height and its range.

Solution:
Note: This solutions uses g=10m/s/s

A rocket is launched at $70^{\circ }$ above horizontal presumably from rest on the ground. It has a constant acceleration of 8 m/s/s in this direction.

It means that the rocket is gaining velocity in both the horizontal and vertical direction.

We choose the origin at the point on the ground where the rocket is launced. The y-axis is positive upward and the x-axis is positive towards the right in the direction the rocket moves.

The rocket accelerates for 6.5 s. At this instant both the x-component and y-component of the velocity are positive.

After that the rocket is in a free fall. It means that the x-component of the velocity is constant and the y-component decreases at a rate of 10 m/s every second.

When the y-component of the velocity becomes zero the rocket is at its maximum height and the direction of its velocity is horizontal. Then the vertical component of the velocity continues to decrease, the y-component of the velocity becomes negative and the rockets speeds up towards the ground.

During the first 6.5 s the rocket gains in both components of the velocity because the acceleration has two non-zero components.

$a_{x}$ = 8 cos70° = 2.7 m/s/s

$a_{y}$ = 8 sin70° = 7.5 m/s/s

Now we can determine the velocity at the end of this interval assuming the initial velocity to be zero:

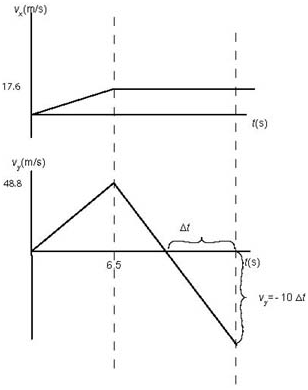
$v_{x}$ = 2.7 × 6.5 = 17.6 m/s/s

$v_{y}$ = 7.5 × 6.5 = 48.8 m/s/s

Now we are ready to draw the two graphs.

The $v_{x}$ - t graph is initially a straight line with a slope of 2.7 m/s/s and after t = 6.5 s the graph becomes a flat line because the horizontal component of the velocity is constant in free fall.

The $v_{y}$ - t graph is initially a straight line with a slope of 7.5 m/s/s and after t = 6.5 s the graph is a straight line with the slope equal to - 10 m/s/s. See the graphs.

The velocity decreases from 48.8 m/s 10 m/s every second after t = 6.5 s. How long does it take before the y-component becomes zero?

It takes 4.88 s.

Therefore it takes a total of 6.5 + 4.88 = 11.4 s for the rocket to reach the highest point in its path.

We can determine the maximum height from the graph. It is the area under the graph ½ × 11.4 × 48.8 = 278 m.

Now we need to determine the horizontal range. We can find it from the $v_{x}$ - t graph if we know how long is the rocket in the air. We know that it took 11.38 s to reach the maximum height of 278 m.

Now we have to find out an interval of time t the rocket moves down: the displacement is equal to - 278 m. The displacement is the area of the triangle and so - 278 = ½ $\Delta t(-10\Delta t$). From this equation we find that $\Delta t$ = 7.5 s.

Thus the total time in the air is 11.4 + 7.5 = 18.9 s.

Now the area under the $v_{x}$ - t graph is equal to ½ × 6.5 × 17.6 + 17.6 × (18.9 - 6.5) = 57.2 + 218.2 = 275.4 = 275 m.

• Back to Projectile Motion
  
  
• Back to Exercises on Projectile Motion