Proj Motion EX 9

Helena Dedic

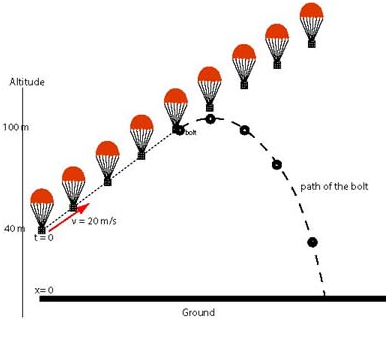
A balloon is launched from the ground. By the time it rises to a height of 40 m its velocity is 20 m/s in the direction of 37° above horizontal. Let us choose to call this time t = 0 and this horizontal position x = 0. Assume the balloon maintains this velocity and that, as it reaches 100 m above ground, a bolt drops from the balloon. Use v - t graphs to solve the following:

a. When will the bolt hit the ground counting from what we called t = 0?

b. How far away will it land? Compute horizontal distance counting relative to x = 0.

c. With what velocity will it land?

Solution:

We will begin to follow the flight of the balloon at the moment it is still 40 m above the ground--at which time we are told it is rising with constant velocity (as illustrated by the consecutive images of the balloon in the diagram below).

When the balloon reaches height (altitude) 100 m, a bolt becomes loose and falls free. Thus while the balloon continues to move with constant velocity, the bolt goes into free fall.

Still rising, it slows down until it reaches its maximum height 
and then begins to speed-up towards the ground. 

Let's choose coordinate system with origin on the ground just below the balloon at the time it is still 40 m above ground. The positive y-axis points upwards and the positive x-axis points to the right.

Now, the bolt--still attached, moves with the the velocity of the balloon between the heights 40 m and 100 m. In other words, until they have risen the additional 60 m, the bolt and balloon move together. Thus in the time it takes to rise the additional 60 m, they will both have covered the same horizontal distance (to the right).

Thus when the bolt becomes loose it still has the velocity of the balloon; in particular, both components of velocity are positive.

We know from this moment onward the vertical component of velocity of the bolt begins to decrease at a rate of 10 m/s every second--while the horizontal component remains constant.

When the vertical component becomes zero, the bolt will have reached the highest point along its path--which is somewhat more than 100 m (since the bolt is rising at the time of its release).

Afterwards however the vertical component becomes negative and continues to decrease at a constant rate of 10 m/s/s. The diagram below illustrates our understanding of the problem:

Since the velocity is 20 m/s and has direction 37° above horizontal the components of velocity are as follows:

vx = 20 cos (37°) = 16 m/s

vy = 20 sin (37°) = 12 m/s

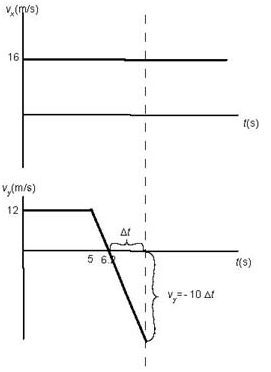
The $v_{x}$ - t graph is a flat line through 16 m/s because the horizontal component of velocity is constant. The $v_{y}$ - t graph begins as a flat line through 12 m/s (balloon moves at constant velocity) but then, at some time t, becomes the line with negative slope - 10 m/s/s (bolt is in free fall).

Can we calculate this time t? Now, the bolt moves 60 m (with the balloon) in the vertical direction and the vertical component of velocity is 12 m/s. This means that t = 60/12 = 5 s. Indeed, it is easy to see this agrees with the vy - t graph which is shown below:

When the graph crosses the t-axis the bolt is at its maximum height: 
the vertical component of velocity is zero. 

How long does it take before the y-component of velocity decreases from 12 m/s to 0 when the rate of decrease is 10 m/s every second?

It takes 12/10 = 1.2 s.

Thus the bolt moves up during only 1.2 s (velocity is positive), in which time it covers a distance of ½ • 1.2 • 12 = 7.2 m (which is the area under the graph).

At this moment (6.2 s into the flight) the bolt has moved up 60 m + 7.2 m from an altitude of 40 m.

Thus at the maximum height the bolt is at 107.5 m above ground and it took 6.2 seconds to get there.

Now we have to find out how long ($\Delta t$) it will take to fall 107.2 m. Using ½ • $\Delta t$ • (-10 • $\Delta t$) = - 107. 2 we find $\Delta t$ = 4.55 s. Therefore the bolt will land at t = 4.55 + 6.2 = 10.75 s.

We can now determine the velocity with which the bolt will land.

The y-component of velocity is $v_{y}$ = -10 • $\Delta t$ = -45.5 m/s. The x-component of the velocity remains the same and thus the velocity is:

v = (16, - 45.5) m/s = 16 i - 45.5 j m/s

From the $v_{x}$ - t graph we find the bolt travels a horizontal distance of 16 × 10.75 = 172 m.

• Back to Projectile Motion
  
  
• Back to Exercises on Projectile Motion