Rotational Kinetic Energy and Moment Of Inertia

Kreshnik Angoni

ROTATIONAL KINETIC ENERGY AND MOMENT OF INERTIA

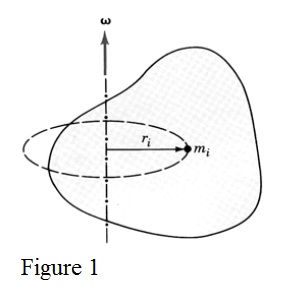
The figure 1 shows a body rotating with angular velocity $\overrightarrow{\omega }$ around a fixed axis. As each point is moving with a different linear velocity we must find the kinetic energy of each point and make the sum. The linear velocity of the particle with mass $m_i$ at distance $r_i$ from the rotation axis is $v_i=\omega r_i$ and its kinetic energy is

$K_i=\frac{1}{2}{m}_i{v_i}^2=\frac{1}{2}{m}_i{r_i}^2{\omega }^2$

The total kinetic energy of the body is

$K=\sum _i{K}_i=\frac{1}{2}{\omega }^2\sum _i{m}_i{r_i}^2$

This expression can be rewritten in form

$K=\frac{1}{2}I{\omega }^2$
where $I=\sum _i{m}_i{r_i}^2$

The quantity $I$ is called the moment of inertia of the body with respect to the axis of rotation. The numerical value of $I$ depends on the way that the mass of the body is distributed spatially with respect to considered axis. A quick comparison of the previous expression with $K=\frac{1}{2}m{v}^2$ allows us to figure out that, in a rotational motion, $I$ is playing the role of the mass for translational motion. So, we can derive that the moment of inertia is a measure of the resistance a body presents to the change of its rotational status of motion, or, in other terms, to its existing angular velocity.

One may easily feel the resistive effect of the moment of inertia by trying to rotate a hammer. When one holds it by the wooden end, it is more difficult because there is a bigger mass at the free end (i.e.: bigger moment of inertia), compared to holding it by the metallic end (less mass at the same distance = smaller moment of inertia).

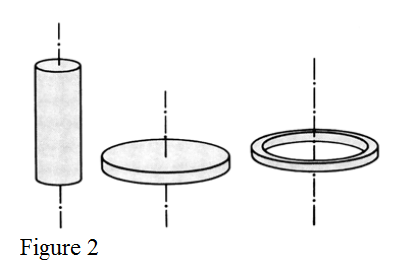
Straight from the definition $I=\sum _i{m}_i{r_i}^2$, we see that the same mass located at a larger distance from the rotation axis produces a bigger moment of inertia. So, one may guess that, for the same mass, the moment of inertia with respect to the central axis of symmetry for a ring, a disk, and a cylinder (figure 2) are different, and $I_{ring}>I_{disk}>I_{cylinder}$. The center of mass of the body is a physical concept that helps to find the $I$-value for any position of the rotation axis.

Center of Mass

When a wheel is rolling, each point on the rim participates in two types of motion; one translational, defined by the translation of the central point, and one rotational, around this central point. The same applies for any rolling object. The rolling motion is an example where a translation and a rotation happen at the same time. The center of mass (CM) is a key concept for the study of these composed motions. The CM of a system is a point (not necessarily part of system) at which translational motion is representative for all particles of the system.

A wrench spinning over a frictionless surface. The CM is moving at constant velocity.

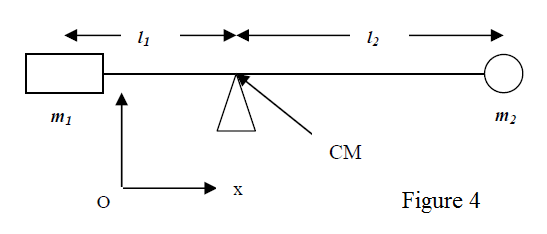
A simple way to find the center of mass is by putting the object on a support and finding the position where it remains at equilibrium (figure 4). We will see that the condition for rotational equilibrium is

$m_1{l}_1=m_2{l}_2$

and this defines the position of the CM for the object in fig. 4.

By using the coordinates on the x-axis of the x-y coordinate system, we get

$l_1=x_{CM}-x_1$

and $l_2=x_2-x_{CM}$

With this, we can rewrite our first equation as

$m_1(x_{CM}-x_1)=m_2(x_2-x_{CM})$

which can be simplified to $x_{CM}(m_1+m_2)=m_1{x}_1+m_2{x}_2$

From this, we get

$x_{CM}=\frac{m_1{x}_1+m_2{x}_2}{(m_1+m_2)}$

And if there are $n$ particles:

$x_{CM}=\frac{\sum _{i=1}^n{m}_i{x}_i}{\sum _{i=1}^n{m}_i}$

The previous expression is simply the x-component of the more general form

${\overrightarrow{r}}_{CM}=\frac{\sum _{i=1}^n{m}_i{\overrightarrow{r}}_i}{\sum _{i=1}^n{m}_i}=\frac{\sum _{i=1}^n{m}_i{\overrightarrow{r}}_i}{M}$

where $M$ is the mass of all particles in system. By deriving this equation, we get

${\overrightarrow{\upsilon }}_{CM}=\frac{\sum _{i=1}^n{m}_i{\overrightarrow{\upsilon }}_i}{M}$

By rewriting this expression as $M{\overrightarrow{\upsilon }}_{CM}=\sum _{i=1}^n{m}_i{\overrightarrow{\upsilon }}_i$ and deriving again versus time, we get

$M\frac{d{\overrightarrow{\upsilon }}_{CM}}{dt}=\sum _{i=1}^n{m}_i\frac{d{\overrightarrow{\upsilon }}_i}{dt}$

$M{\overrightarrow{a}}_{CM}=\sum _{i=1}^n{m}_i{\overrightarrow{a}}_i$

$M{\overrightarrow{a}}_{CM}=\sum _{i=1}^n{\overrightarrow{F}}_i={\overrightarrow{F}}_{ext}$

${\overrightarrow{F}}_{ext}=M{\overrightarrow{a}}_{CM}$

This last equation shows that the center of mass moves as if it were a particle with mass M at its location.

For an isolated system of particles, due to Newton's Third Law, $\sum _{i=1}^n{\overrightarrow{F}}_i=0$ and ${\overrightarrow{F}}_{ext}=0$. In this case, the CM keeps its state of motion for all time; either at rest or in uniform motion. The CM of the wrench in fig. 3 moves with constant velocity (in a straight line) because the net exterior force on wrench is zero. If thrown vertically, its "translational" motion would be along a parabola, like that of a particle with mass $M$.

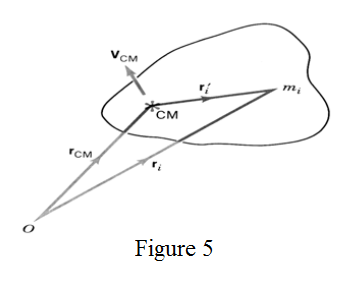
Now, let's consider the total kinetic energy of an object that is participating in a rotational motion and a translational motion (the wheel is an example). The velocity of the $i^{th}$ particle ${\overrightarrow{\upsilon }}_i=\frac{d{\overrightarrow{r}}_i}{dt}$ can be expressed as

${\overrightarrow{\upsilon }}_i={\overrightarrow{\upsilon }}_{CM}+{{\overrightarrow{\upsilon }}_i}^{\prime }$

where ${{\overrightarrow{\upsilon }}_i}^{\prime }$ is the relative velocity versus the CM.

Its kinetic energy is

$K=\frac{1}{2}{m}_i{\overrightarrow{\upsilon }}_i\cdot {\overrightarrow{\upsilon }}_i$

The kinetic energy of a body is equal to the sum of the kinetic energies of all its particles. So, we can calculate it as follows

$K=\sum _i{K}_i=\sum _i\frac{1}{2}{m}_i{\overrightarrow{\upsilon }}_i\cdot {\overrightarrow{\upsilon }}_i=\sum _i\frac{1}{2}{m}_i({\overrightarrow{\upsilon }}_{CM}+{{\overrightarrow{\upsilon }}_i}^{\prime })({\overrightarrow{\upsilon }}_{CM}+{{\overrightarrow{\upsilon }}_i}^{\prime })=\sum _i\frac{1}{2}{m}_i(\underset{CM}{\overset{2}{\upsilon }}+{\upsilon }_i{\text{'}}^2+2{\overrightarrow{\upsilon }}_{CM}{{\overrightarrow{\upsilon }}_i}^{\prime })=\frac{1}{2}\underset{CM}{\overset{2}{\upsilon }}\sum _i{m}_i+\frac{1}{2}\sum _i{m}_i{\upsilon }_i{\text{'}}^2+{\overrightarrow{\upsilon }}_{CM}\sum _i{m}_i{{\overrightarrow{\upsilon }}_i}^{\prime }$

Then,

$K=\frac{1}{2}\underset{CM}{\overset{2}{\upsilon }}\sum _i{m}_i+\frac{1}{2}\sum _i{m}_i{\upsilon }_i{\text{'}}^2=K_{CM}+K_{rel}$

This expression is very general. It tells us that the total kinetic energy of a body in rotational motion is the sum of the translational kinetic energy of its CM plus the rotational kinetic energy with respect to its CM. Note that the ${\overrightarrow{\upsilon }}_{CM}\sum _i{m}_i{{\overrightarrow{\upsilon }}_i}^{\prime }$ disappeared in this step. To explain this, we use the previous equation

${\overrightarrow{\upsilon }}_{CM}=\frac{\sum _{i=1}^n{m}_i{\overrightarrow{\upsilon }}_i}{M}$

$\sum _{i=1}^n{m}_i{\overrightarrow{\upsilon }}_i=M{\overrightarrow{\upsilon }}_{CM}$

$\sum _{i=1}^n{m}_i{{\overrightarrow{\upsilon }}_i}^{\prime }=M{{\overrightarrow{\upsilon }}_{C^{\prime }M}}^{\prime }=0$

because ${{\overrightarrow{\upsilon }}_{C^{\prime }M}}^{\prime }$ is the velocity of the CM versus the CM (a given point cannot move with respect to itself).

$K_{CM}=\frac{1}{2}\underset{CM}{\overset{2}{\upsilon }}\sum _i{m}_i=\frac{1}{2}M\underset{CM}{\overset{2}{\upsilon }}$

is the translational kinetic energy of the CM and

$K_{rel}=\frac{1}{2}\sum _i{m}_i{\upsilon }_i{\text{'}}^2$

is the rotational kinetic energy of relative motion about the CM.

Parallel Axis Theorem

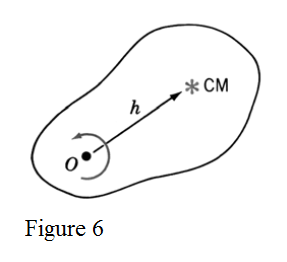
This theorem relates the moment of inertia $I$ about some axis to the moment of inertia $I_{CM}$ about the axis passing through the center of mass and parallel to the one being examined. Let's find this relation. Consider an axis $O_z$ perpendicular to the section in figure 6 and passing through the point O at a distance $h$ from the CM of the body. Suppose that the body is moving around point $O$ with angular velocity $\omega$. Each point of the body is moving with the same angular velocity $\omega$ versus the CM, too. Note that a body in motion possesses a given numerical value of kinetic energy no matter the method used to calculate it. It's logical that we use the simplest method at our disposal to calculate it. In this case, we calculate the kinetic energy by using the previously-derived expression

$K=K_{CM}+K_{rel}=\frac{1}{2}M\underset{CM}{\overset{2}{\upsilon }}+\frac{1}{2}{I}_{CM}{\omega }^2$

In our case (see fig. 6) the CM is rotating around point $O$ with angular velocity $\omega$. So, its translational or linear velocity is

${\upsilon }_{CM}=\omega h$

By substituting this into the previous equation, we get

$K=\frac{1}{2}M{\omega }^2{h}^2+\frac{1}{2}{I}_{CM}{\omega }^2=\frac{1}{2}(I_{CM}+M{h}^2){\omega }^2$

By using the expression for kinetic energy for the axis $O_z$ passing by $O$, we have

$K=\frac{1}{2}{I}_{O_z}{\omega }^2$

Since the results of the two previous equations must be the same, we get

$I_{O_z}=I_{CM}+M{h}^2$

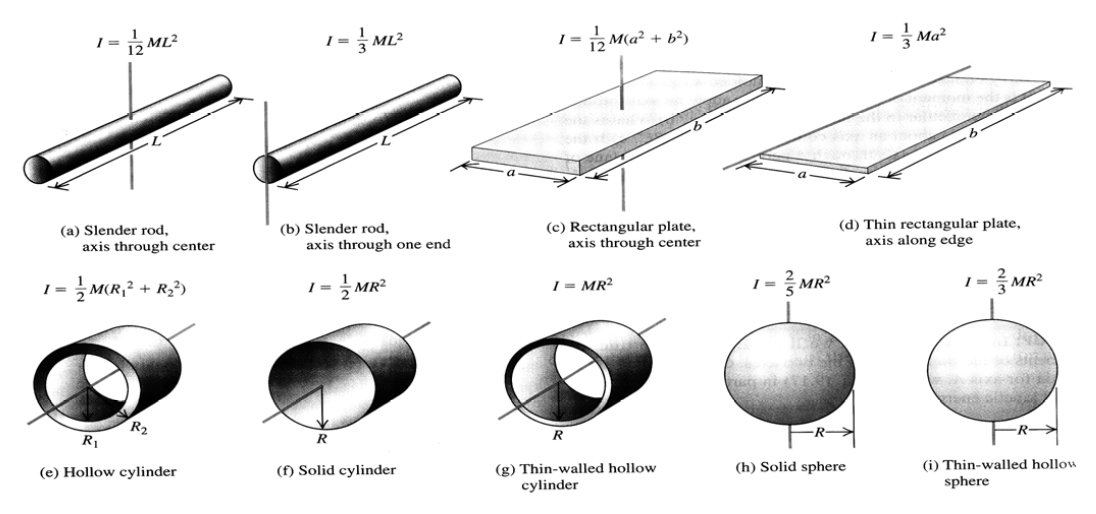
The moment of inertia passing through the CM for some basic forms of bodies are given in tables. So, by the use of this new formula, one may easily calculate I-values for parallel axes passing by different positions on the body. The following table contains some basic expressions for the moment of inertia $I_{CM}$.

CONSERVATION OF MECHANICAL ENERGY (TRANSLATION AND ROTATION)

The principle for the conservation of mechanical energy applies in situations when there is no external work done over the system constituents. This principle applies no matter the kind of motion a system achieves. Let’s apply this principle for a sphere with mass $M$ and radius $R$ that rolls without slipping on an inclined plane (figure 7).

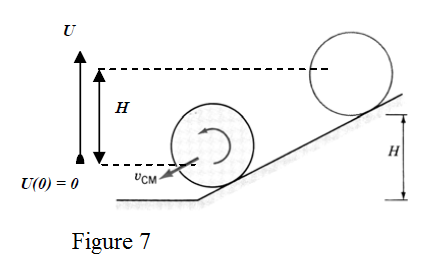
The principle tells that the mechanical energy $E(H)$ of the sphere before starting to roll, at height $H$, is equal to its mechanical energy at any level $E(h)$. We will refer to the end of inclined plane (h=0). So, the principle of mechanical energy conservation is written

$E(H)=E(0)$

At H-level, the sphere posses only potential energy;

$E(H)=MgH$

Notes: a) The expression $E(H)=U(H)=MgH$ means that we have fixed the 0-value for potential energy at the lower end of inclined plane. More precisely, the origin for potential energy is at the level of the sphere's CM when the it is at the bottom of the plane because the potential energy of the sphere is equal to that of a particle with mass M at its CM.

b) Remember that, the potential energy of sphere ($MgH$) belongs to the system sphere-earth and this means that the gravitation force is not an external force for our system.

At the end of inclined plane (h = 0) the sphere is participating in two motions, rotation around its CM and translation like its CM. So, its kinetic energy is

$K=\frac{1}{2}M\underset{CM}{\overset{2}{\upsilon }}+\frac{1}{2}{I}_{CM}{\omega }^2$

As its potential energy is $U(0)=0$, we get

$E(0)=K(0)+U(0)=\frac{1}{2}M\underset{CM}{\overset{2}{\upsilon }}+\frac{1}{2}{I}_{CM}{\omega }^2$

Then, by using the principle of conservation,

$E(H)=E(0)$

$MgH=\frac{1}{2}M\underset{CM}{\overset{2}{\upsilon }}+\frac{1}{2}{I}_{CM}{\omega }^2$

As ${\upsilon }_{CM}=\omega R$, we get

$MgH=\frac{1}{2}M\underset{CM}{\overset{2}{\upsilon }}+\frac{1}{2}{I}_{CM}\frac{\underset{CM}{\overset{2}{\upsilon }}}{R^2}$

Therefore,

${\upsilon }_{CM}=\sqrt{\frac{2MgH}{M+\frac{I_{CM}}{R^2}}}$