Static Equilibrium EX 4
The rod is being studied. Three forces act on the rod: the tension in the wire ; the load and the support at the hinge . The wire is 60 cm long and it appears to be horizontal. It is attached in the middle of the rod. Thus, the wire, the wall and the rod form a right angle triangle with hypotenuse 1 m and one side of 60 cm. From this information, we can compute the angle between the rod and the wall:
The diagram below shows the forces and the lever arm for each of the forces. Note that the load acts 2.00 m from the pivot and the wire pulls at a distance 1 m from the pivot. The torque exerted by the support is equal to zero because it acts at the pivot.
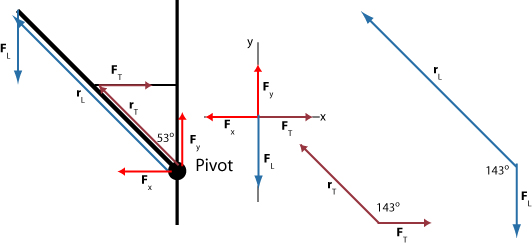
The rod is in equilibrium and so
We will first compute the torques:
| Force | Direction | Torque |
|---|---|---|
| CW | ||
| CCW | ||
| 0 |
Solving for ,
Then we will determine the components of the support at the pivot:
| Forces | x-component | y-component |
|---|---|---|
| 400 N | 0 | |
| 0 | -200 N | |
| 0 | 0 |
Solving the two equations we find