The Exponential Function and Its Applications in Science
Don Hetherington
The text books referred to in this module are:
- James Stewart: Single Variable Calculus, fourth edition (Brooks/Cole Publishing Company)
- Harris Benson: University Physics, revised edition (John Wiley and Sons Inc.)
- Reger, Goode and Mercer: Chemistry: Principles & Practice, second edition (Saunders College Publishing)
- Purves, Sadava, Orians and Heller: Life: The Science of Biology, sixth edition (W.H. Freeman and Company)
Properties of the Exponential Function
Geometric Progression and the Exponential Function
reference: Stewart, sections 1.5 and 3.1
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| --- | --- |
Consider the pairs of values for x and y shown in the table. Note that each time x increases by 1, the value of y is increased by a factor of 2. Any such function in which the dependent variable increases by a constant factor is called a “geometric progression”. In this case, the function can be generated by the expression:
which is an exponential function with base 2.
If we take the natural log of both sides of this equation, we get:
If we then take the exponential of both sides, we find:
where the parameter λ = ln2
From this we can see that any geometric progression can be represented by an exponential
function with base e.
| Exercise 1.1
Consider a geometric progression where y increases by a factor of 5 for each increase by 1 of x. |
Derivative of the Exponential Function
A key property (in fact, the defining property for the base e) of the exponential function is that it is it’s own derivative.
(See Stewart, section 3.1)
This leads to a very important result that has many applications in the sciences. Whenever a quantity is changing in such a way that the time rate of change is proportional to the quantity itself, the quantity can be represented by an exponential function of time. (Note that since the independent variable now represents time, the symbol x is replaced by t.) For example, suppose y is a quantity that has the property:
This is equivalent to:
where is the proportionality constant.
Dividing by y and multiplying by dt, we get:
Integrating both sides of the equation gives:
ln y = λ t + k where k is an arbitrary constant.
Taking the exponential of each side of the equation gives:
where and represents the value of y at t = 0.
| Exercise 1.2
Find the derivative, dy/dt, of and show that it is proportional to y. |
Exponential Decay
|
Now consider a geometric progression where the factor is ½ (ie the dependent variable changes by a factor of ½ for each increment of 1 of the independent variable). The expression is:
Again taking the natural log of both sides we get:
Finally taking the exponential of both sides:
where
This type of function is called an exponential decay
and is characterized by the fact that the dependent variable decreases by a constant factor each time the independent variable increases by a certain amount. As a consequence, the exponent is negative.
| Exercise 1.3
Let (a) Calculate y for x = 1, 2, 3, 4, 5. (b) In the corresponding geometric progression, what is the constant factor by which y changes each time x increases by 1? |
Now consider the case where the dependent variable decreases with time in proportion to its
own value.
As seen in section 1.2, the solution to this “differential equation” is an exponential, but this time with a negative exponent.
This is called an exponential decay and is known as the “decay constant:
Note that when the independent variable is time, the decay constant must have the units of inverse time (e.g. )
The equation for an exponential decay is often written using a different parameter called the “time constant” which is defined as:
The exponential decay equation becomes:
and has the same units as t .
Substituting for t, we can see that:
for t = 0
for
for t = 2
for t = 3 etc.
In other words, the decay follows a geometric progression where for each interval of time ,
the value of y falls by a constant factor of 1/e. This holds true no matter when you set the time t = 0.
| Exercise 1.4
|
Finally consider what we get when we take the natural log of each side of the equation:
Comparing this to the generic equation for a straight line, y = b + m x, (note that the variable y
in this equation is different than the y in all other equations) we see that a graph of ln y vs t
will yield a straight line with slope ( or ). This is a powerful experimental tool for demonstrating whether or not a certain measured quantity follows an exponential decay.
| Exercise 1.5
The table shows the values of some quantity z as a function of time.
| ||||||||||||||||||||
| (a) Plot an accurate graph of z vs t . Find the time constant by reading from the graph the values of t at which , and . | ||||||||||||||||||||
| (b) Calculate ln z for each value of z and plot a graph of ln z vs t. Draw a straight line through the points on this graph. Find the slope and intercept of the graph and from them calculate the values of and . Compare these to the values found in part (a). |
Applications in Physics
There are many physical processes that follow an exponential function. As discussed in section 1, this occurs whenever the rate of change of some quantity is proportional to the quantity itself.
Radioactive Decay
Reference: Benson, section 43.4
The atomic nucleus is made up of neutrons and protons. Only nuclei with certain ratios of the number of neutrons to the number of protons (called isotopes) are stable, all others will change spontaneously into another combination by giving off a quantum of radiation. These radiations were called alpha, beta and gamma rays by the early researchers. We now know
that the alpha ray is a helium nucleus, the beta ray is an electron or positron and the gamma ray is a high energy photon.
Because this process is governed by quantum mechanics, it happens at random. In a sample of radioactive nuclei, there is no way to know which individual nucleus will decay next or when the next decay will occur. All that is known is that there is a certain probability that a given nucleus will decay within a certain period of time. The probability of decay per unit time is and the probability in a period of time t is t. Since the probability is exactly the same for all nuclei of the same species, then the number of nuclei that will decay during the next unit of time is N t where N is the number of nuclei present. Since the number of nuclei present in the sample decreases by this same amount, then:
N = - N t
or,
To get the instantaneous rate of decay, we let approach 0 in the usual way and get:
Note that if is the probability of decay in one second, then it has units of .
In a real experiment, one usually measures the number of particles or “rays” emitted by
the sample per unit time. Assuming that each particle emitted represents the decay of one
nucleus, this is the same as the number of nuclei that decay per second and is known as the
decay rate R. It is given by:
R = λ N
Since the decay process is random, this equation only gives the most likely or average value of the decay rate at a given moment. Actual measurements of the number of particles emitted will vary statistically with a “Normal” distribution that has a standard deviation or
uncertainty of σ = ± where is the number of decays in a time interval .
As discussed in section 1.3, since the rate of change of the number of nuclei is proportional to the number itself, then both the number of nuclei in the sample and the decay rate follow an exponential decay function:
|
|
and
|
|
where is the number of nuclei at t = 0 and is the decay rate at t = 0.
Note that the word “decay” is used in two different but related ways in this text. When a single nucleus changes to another nucleus, it is said to “decay”. On the other hand, when the number of nuclei decreases with time the number of nuclei is said to “decay” according to the exponential decay function.
| Exercise 2.1
(a) By finding the derivative of N, show that satisfies the differential equation (b) Substitute t = 0 into the expression for N to show that is the number of nuclei at t =0. |
| Exercise 2.2
A certain radioactive nucleus has a decay probability of 0.10 . (a) From an original sample of one million nuclei, how many will be left after one minute? (b) How many nuclei will have decayed in this time? (c) Why is it not correct to use to calculate the answer in part (b)?
|
| Exercise 2.3
A certain radioactive nucleus decays at a rate such that after one day, 10% of the sample has decayed. What is the decay probability, , for this nucleus in units of ? |
Half-life
We have seen in section 1.3 (Exponential Decay) that an exponential decay can be characterized by the time constant, , which is equal the inverse of the probability of decay, , and represents the time for the number of nuclei to decrease by a factor of 1/e of its initial value to . (e is the base of the natural logarithm.) In the first time interval , N falls from to . In the next time interval , N falls a further factor of 1/e to a value of .
In radioactive decay, a more commonly used time interval to characterize the rate of decay is the half-life which is defined as the time it takes for the number of nuclei to decay to half its initial value. The symbol for half-life is T½ . In the first half-life, the number of nuclei falls to . In the second half-life, it falls to and so on.
| Exercise 2.4
|
| Exercise 2.5
(a) What fraction of the original sample will be left after 1 year? (b) How long does it take for the number of nuclei to be reduced to 1% of its original value? (c) What is the activity (number of decays per second) of a sample of 1.0 gram of pure Co . (N.B. Assume for simplicity that the atomic mass is exactly equal to the atomic mass number in atomic mass units.) |
Exercise 2.6
|
Capacitor Discharge
reference: Benson, section 28.4
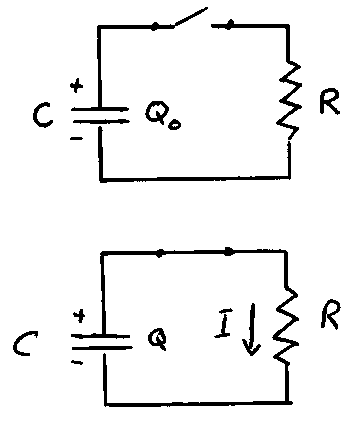
Another physical situation where the rate of change of a quantity is proportional to the quantity itself occurs in electric circuits when a capacitor discharges through a resistor. Consider the circuit shown. Suppose that the capacitor C carries a charge on each of its plates of + or - . When the switch is closed at t = 0, charge begins to flow through the resistor until the charge on the positive plate of the capacitor completely neutralizes the charge on the negative plate. Throughout this process, the potential difference across the capacitor is the same as the potential difference across the resistor:
From conservation of charge, the rate at which charge flows from the capacitor is equal to the current flowing through the resistor. Since this serves to reduce the amount of charge on the capacitor, the rate of change is negative:
Combining this with the equation above, we have:
or
In other words, the rate of change of Q is proportional to Q with a proportionality constant of - 1/RC. The solution of this differential equation is:
where: = the charge at t = 0 and is the time constant.
| Exercise 2.7
In an RC discharge circuit, R = 6.0 k and C = 100 F. The charge at t = 0 is 50 mC. |
| Exercise 2.8
Show that the current (I = - dQ/dt) through the resistor in an RC discharge circuit also follows an exponential decay. |
| Exercise 2.9
The current in an RC discharge circuit falls to 10% of its initial value in 5 seconds. |
Damped Oscillations
In Physics NYC (Waves and Modern Physics), you studied the simple harmonic motion of a mass on a spring and the simple pendulum. The motion of all such systems is described by the equation: x = A cosω t where A is the amplitude of the motion and its period is:
is called the angular frequency and is measured in rad/s. For simplicity we will assume that
x = A at t = 0 (ie. the phase angle is zero).
You also know that if a frictional force is added to the system, the amplitude of the oscillations decays exponentially. The motion of the system is said to be “damped” and is described by:
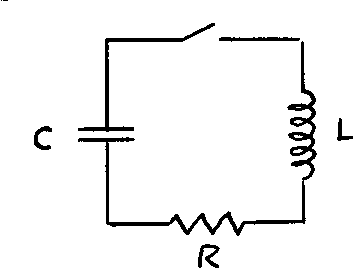
The time constant where m is the mass and is a measure of the amount of friction.
The angular frequency, ’ is slightly different from the undamped frequency .
Remarkably, the electrical circuit shown also exhibits damped harmonic motion. If the capacitor is given an initial charge Q_0 , the charge Q is described by the equation:
| |
where
and
| Exercise 2.10
An RLC circuit has the values L = 20 mH, C = 50 F and R = 0.5 . (a) Calculate the “half-life” of the amplitude of the oscillations of this circuit. Does this
result depend on the initial charge ? (b) How many oscillations does the circuit go through while the charge amplitude falls to 0.5 of its initial value ? |
Applications in Chemistry and Biology
First Order Reaction Rates
Reference: Reger, Goode and Mercer, section 13.3
In a chemical reaction, the reaction is said to be first order with respect to a certain reactant when the rate at which that reactant is used up is proportional to its concentration. Let the concentration of a reactant be [A], then the change of concentration, over a time period in a first order reaction will be:
where k is called the rate constant (equivalent to the symbol in the previous section). The
negative sign indicates that the concentration of the reactant decreases with time.
For an infinitesimally short period of time, the instantaneous rate of change is:
which we can solve to get:
Taking the natural logarithm of both sides of the equation, we get:
or
This equation shows that a graph of ln[A] vs t yields a straight line with a slope of -k and an intercept of . This provides a good method of analysing data to verify whether or not it represents an exponential decay.
| Exercise 3.1
The “half-life” (T½) of a first order reaction is defined as the time it takes the concentration to fall to half of its initial value. (a) Show that T½ = 0.693/k. (b) Plot a graph of the ratio for a first order reaction with a half life of 100 ms. (c) Plot a graph of the natural logarithm of for the same reaction. |
| Exercise 3.2
The concentration of a reactant in a certain chemical reaction is shown in the table as a
function of time.
|
Population Growth
reference: Purves et al, chapter 54
Let us consider the population of some species starting with just two individuals. Suppose
these two individuals produce four offspring in their lifetime. Suppose that the next generation follows the same pattern and produces four offspring for each pair for a total of eight. These go on in their turn to produce sixteen offspring and so on. Each generation, the population increases by a factor of two. As discussed in section 1, this pattern represents an exponential growth. The rate of growth of the population is proportional to the present population:
where N is the number of individuals and r is called the intrinsic growth rate. As usual, the solution to this equation is:
| Exercise 3.3
Consider the scenario described above and assume that this is a human population where a generation represents about 20 years. Further assume that the two parents die after producing their four offspring so that the population follows a simple geometric progression: 2, 4, 8, 16,... with a time interval of 20 years (ie. the population doubles every 20 years). Calculate the intrinsic growth rate, r, for this population in units of people per year. |
| Exercise 3.4
A bacteria culture starts with bacteria and the growth rate is proportional to the number of bacteria. After 2 hours the population is . (b) Find the number of bacteria after 3 hours. (c) Find the rate of growth after 3 hours. (d) How long does it take for the number of bacteria to double? (e) Suppose the bacteria are growing in a dish that can accommodate a maximum of bacteria and that the population continues to increase exponentially right up to the moment that the dish is full. How long does this take from the starting point with bacteria? (f) How long does it take to fill the first half of the dish? How long does it take to fill the second half of the dish? |
In real situations, of course, no population can continue to grow exponentially for ever. For example, consider this quotation from the text Life, The Science of Biology, sixth edition by Purves et al.
“... a single pair of Atlantic cod and their descendants, reproducing at the maximum rate
of which they are capable, would fill the Atlantic Ocean in 6 years.”
Obviously, life for the cod fish, as for every other species, is not so simple. In real life, population growth is limited by factors such as food sources, predators, space, etc. For a discussion of more realistic population growth patterns, see your biology text.