What is Dynamics?
Kreshnik Angoni
Dynamics answers the question:
“Why does an object move or stay at rest?”.
It operates with two main concepts:” the force and the mass ”.
The force describes the action which attempts to change the object velocity while its mass describes the object reaction versus “forced change of its velocity”.
The combination of these two major concepts makes possible to explain why the considered object is in a given status of motion (given acceleration and velocity).
FORCE
- Initially, this word was introduced to describe a “push or pull” action exerted on a body. People observed that the effect of “push or pull” force is to “deform” the body, to ”change its velocity ” or the two together.
- The “push or pull” forces are exerted when one uses ropes, springs, collisions...; i.e. in all situations where there is a contact between the source of action and the object that suffers the force.
The development of physics showed the existence of forces exerted without contact (Ex: Magnetic, electrostatic, gravitational) between the source and the object that suffers the force.
Meanwhile, no matter what type it is (contact or no contact), the effect of a force exerted on a body is the same: deformation, velocity change or the two together. So, a best definition of force would be related with its effects. One says that a force is exerted on a body when it is deformed, changes its motion or the two of them together.
Note that this definition of force is seen only from the point of view of the body that suffers it.
Important Note: Dynamics neglects the deformations and deals only with changes in the motion.
- Physics deals with measurable quantities. How to measure force magnitude? By use of the normal method:
a) define a force unit
b) define a procedure for comparison of different forces.
A simple procedure is by use of strings elasticity; spring extension is proportional to the exerted force at its end. One may select a standard spring and define the force unit by referring to spring extension by a unit length, say 1cm. Due to proportionality, a two units force would produce a double extension on the standard spring and so on. So, in principle, there is no problem to define forces numerically. Note that the described method has two relevant drawbacks.
1-It is impossible to produce standard spring that keeps its elasticity unchanged forever.
2-One cannot use springs for measuring forces on atomic or interplanetary scales.
In fact, one has preferred to define the unit of force through the second law of Newton.
This way it is a derived physical unit.

Is the force a vector or scalar quantity?
One can verify easily that the force is a vector quantity by using three spring balances with tied tiles and oriented along different angles and using the vectors’ rules to explain the fact that the point P is at rest.
The special case of a body at rest corresponds to velocity equal to zero.
MASS
We know that the inertia is the propriety of bodies to resist to the changes on their velocity.
The mass is the physical quantity that measures the inertia of a body.
So, the mass of a body tells how difficult is to change its velocity (its magnitude, its direction or both). To achieve the same velocity change, a bigger effort is required in case of objects with bigger mass.
From the definition, it comes out that the mass is an intrinsic characteristic of the whole body and it does not depend on direction.
So, it is a scalar physical quantity.
How to measure the magnitude of mass?
By use of the normal method:
a) define a mass unit.
The standard in the International Office for Measurement Units in Paris is chosen as the unit mass 1kg.
b) Define a procedure for comparison of different masses.
The following is a direct procedure for mass measurement.
One fixes two objects with masses , on two equal massless pucks at rest on two sides of a string kept compressed by use of a string. This set is placed on an air table. The air cushion avoids the friction and balances the gravity. Once one cuts the string, the spring extends and produces two forces with the same magnitude on its sides.
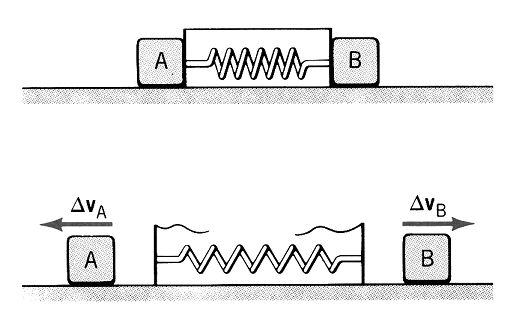
The pucks, that were initially at rest, start to move with velocities , .
One can measure easily these velocities that are equal to the change of velocity itself. As the change of velocity is proportional to the inverse of mass, one gets
and
By using the standard unit mass = 1kg, the described method and the expression:
in principle, one can measure the mass of different objects.
This method for mass measurements is perfect but it is not very simple. In practice, one measures the mass of objects through weight measurements by use of a balance. As we will see, this is not a precise method but is very simple and the precision is good enough for general-purpose measurements.
Insignificant with respect to ,