Work-Energy Theorem EX 9
Jump to navigation
Jump to search
(a) The diagram below shows the forces acting on the mass and a free body diagram. The displacement of the mass is because we chose the initial position of the mass as the origin of the coordinate system ( and ).
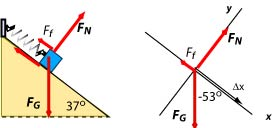
- The work done by the normal force is zero because it is perpendicular to the displacement or because the x-component of the normal force is zero.
- The gravitational force is a constant force. The x-component of the gravitational force is and so we may use . We cannot compute its value because we don't know the value of x.
- Before we compute the work done on the mass by friction we have to first determine the magnitude of the force of friction. Applying the Second Law to the y-components of forces we find that the normal force is 8 N and that, given the coefficient of friction is , the force of friction is . The x-component of the frictional force is . From there we find the work done by friction . Again, we cannot compute the value of this force because we don't know the value of x.
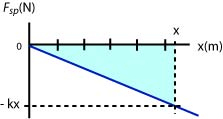
- The force exerted on the mass by the spring is not constant. We have to use a graph to find it. As the block slides down the x-component of the spring force is . Note that on the vertical axis we are plotting the x-component of the spring force which is negative (the graph is below the axis).
The area under the graph is . Therefore .
(b) The net work is zero because the mass starts from rest and stops when it slides down the distance . The change of the kinetic energy is zero.
(c) Knowing that we can compute . By substituting the expressions found above into this equation we write:
Solving for we find
.