Work-Energy Theoremx EX 6

Let's assume that you want to raise the block to some height $h$. Let's further assume that you raise it by pushing the block straight up at constant velocity. In other words the net force exerted on the box is zero. This means that the force exerted by you on the block balances the gravitational force i.e. the magnitude of the force exerted by you is the same as the magnitude of the gravitational force and it points in the direction opposite to the direction of the gravitational force (i.e.: upward). The displacement $\mathrm{\Delta }r$ has magnitude $h$ and also points upward. In this case the work done by you is $W=F_{G}h\cos (0^{\circ })=mgh$.

Now let's assume that you push the block along an incline at constant velocity (note that the angle of inclination of the incline is $\theta$ and that you exert the force in a direction parallel to the displacement. The diagram below shows this situation. A "thumbnail" of a free body diagram is on the right - note that the x-axis points in the direction of the displacement.

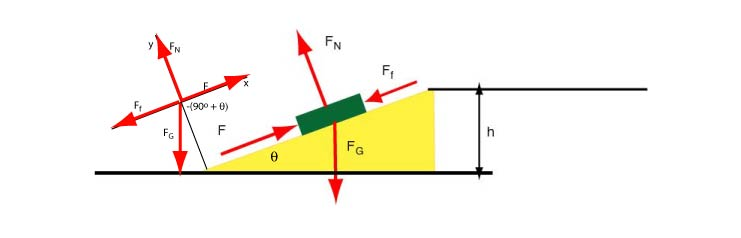
Forming the sum of y-components of the forces, we find that the normal force is equal to

$F_N=-mg\sin (-(90+\theta ))=mg\cos \theta$

The force of friction is then

$F_f={\mu }_{k}mg\cos \theta$

The net work done on the block is zero because the block moves at constant velocity. Since you push the block along the incline to the height $h$, the displacement of the block is equal to

$\mathrm{\Delta }x=\frac{h}{\sin \theta }$

The work done by the force you exert is equal to

$W_F=\frac{Fh}{sin\theta }$

The x-component of the friction is ${F_f}_x={\mu }_{k}mg\cos \theta \cos (180^{\circ })=-{\mu }_{k}mg\cos \theta$. The work done by the force of friction is

$W_{F_f}=\frac{-{\mu }_{k}mgcos\theta h}{\sin \theta }=-{\mu }_{k}mghcot\theta$

The x-component of the gravitational force is ${F_G}_x=mg\cos (-(90+\theta ))=-mg\sin \theta$. The work done by the gravitational force is

$W_{F_G}=\frac{-mg\sin \theta h}{\sin \theta }=-mgh$

Since the net work is zero we can write

$W_F+W_{F_f}+W_{F_G}=0$

Substituting into this equation the expressions for work that we found above we get

$\frac{Fh}{\sin \theta }-{\mu }_{k}mghcot\theta -mgh=0$

Solving for $F$ we find

$F=mg\sin \theta +{\mu }_{k}mg\cos \theta$

Now we can write the work done by $F$ as follows

$W_F=F\mathrm{\Delta }x=\frac{(mg\sin \theta +{\mu }_{k}mg\cos \theta )h}{\sin \theta }=mgh+{\mu }_{k}mgh\tan \theta$

Now we can consider two possibilities:

1. The incline is frictionless or ${\mu }_k=0$: The work becomes $W_F=mgh$. This is the same values for work as we found when the object was simply lifted.
   
2. There is a friction between the block and the incline: In this case the work done by you is larger then the work done by simply lifting it up. We do this because the required force $F$ is smaller.