Dynamics of Circular Motion
Kreshnik Angoni
THE DYNAMICS OF CIRCULAR MOTION
- In kinematics we found that a particle moving at constant speed v around a circle with radius r has acceleration. This acceleration is directed towards the circle center at all times, and has constant magnitude:
So, in vector form, we have:
......... (1)
where
is the unit radial vector (tail at center) defining the direction from origin.
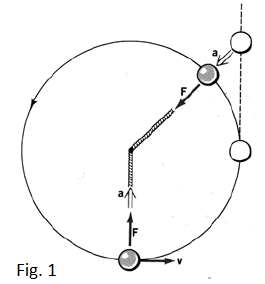
The vector is called centripetal acceleration because it is directed all time versus the circle center. The 2nd law tells that a particle with mass which is moving with centripetal acceleration is under the action of a net force directed along (fig.1)
........ (2)
This force, with magnitude , is called centripetal force because it is directed
all time versus the circle center. Note that it is named only from its direction and
not from its physical origin. A force of gravity, friction, electric …or their sum
can be in the role of a centripetal force.
Note: You must not add a centripetal force in a free body diagram.
- The action of centripetal force consists in not leaving the particle to follow its path along the tangent “as required by its inertia”. As the third law affirms, the particle reacts on this action by a force of equal magnitude, opposite direction and applied on that source itself.
Example 1: A man has fixed an object at a string and rotates it in a horizontal plane.
The net force acting on the object is the sum of his hand force (transmitted by
string via its tension) plus the weight of object. This net force acts as centripetal
force exerted on the object. The object reacts (via the string tension) by a force
with equal magnitude and opposite direction applied on the man’s hand; this is
a centrifugal force acting on the man (who is not in circular motion).
Example 2: A car travels at high speed around a horizontal curved path. The friction force exerted by the
road on the rotating tires plays the role of centripetal force (its source is the road). An equal force
with opposite direction, the centrifugal force, is exerted on the road.
Note: Sometimes, by error, one talks about the centrifugal force exerted on the rotating body. The
example of a passenger inside the rotating car that feels himself pushed “out of circle” is mentioned.
The truth is that the passenger is not hard bounded with the seat to get the centripetal force via the
action of friction straight away. So, due to his inertia he follows his way along the tangent….until
he touches the interior of the door. Then, the door transmits to him the centripetal action and after
that he follows the same circular motion as the car.
Remember: There is no net outward (centrifugal force) exerted on the rotating body…only….centripetal force.
Loop the loop:
SATELLITE MOTION
- The satellite is a small body with mass m that turns around a central body with bigger mass M due to the gravitational interaction. In fact, being the only force exerted on the satellite, the gravitation force is the net force on the small body and it plays the role of centripetal force.
- By equalizing the two expressions for the magnitudes
........(3)
one finds out that:
....... (4)
So, the orbital speed of a satellite:
- a) Depends only on central mass M and not on satellite mass
- b) Decreases with the increase of orbit radius.
- a) Depends only on central mass M and not on satellite mass
- The period of satellite in a fixed (r value) orbit is
........ (5)
- and
........(6)
The expression (6) known as Kepler’s third law shows that the period of different satellites around the same central body depends only from their distance.
This expression is very useful because by measuring the orbit radius and the satellite period one may calculate the mass of the central body. For example, one may calculate the sun’s mass by using the periods and distances of its satellites (planets) or the earth’s mass by using moon’s period and distance from the earth.
See also