Newton's Law of Universal Gravitation

Kreshnik Angoni

The law of Universal Gravitation is formulated by Newton for two point particles with masses $m_{1}$ and $m_{2}$ at a distance r between them. The magnitude of force exerted on one particle by the other one is given by:

 $F_{12} = F_{21} = G \frac{m_{1} m_{2}}{r^{2}}$

The measurements show that the universal constant of gravitation is $G = 6.67 * 1 0^{- 11} N m^{2} / k g^{2}$

The gravitational force is a vector directed versus the source that exerts this force. So, its vector form is:

 $F_{12} = - G \frac{m_{1} m_{2}}{r^{2}} \frac{\vec{r_{21}}}{r_{21}}$

where $\frac{\vec{r_{21}}}{r_{21}}$ (or, ${\hat{r}}_{21}$ ) is the unit vector with tail at mass $m_{2}$ – the source of ${\vec{F}}_{12}$ .

 $F_{21} = - G \frac{m_{1} m_{2}}{r^{2}} \frac{\vec{r_{12}}}{r_{12}}$

$\frac{\vec{r_{12}}}{r_{12}}$ (or, ${\hat{r}}_{12}$ ) is the unit vector with tail at mass $m_{1}$ – the source of ${\vec{F}}_{21}$ .

To apply the gravitational law for two bodies close to each other one must use integration techniques and

the difficulty of calculi depends on the form of the two bodies. But, if the bodied are far enough to each other, one may model them as point particles and apply the law in its original form.

In particular, with some approximations, we are able to model the interaction of earth with an object on its surface as if the whole mass of the earth is concentrated at its center and the objects are at distance $r = R_{e a r t h}$ .

Many experiments have shown that; when several particles interact gravitationally between them the

principle of linear superposition applies. So, inside a system of particles $m_{1}, m_{2}, m_{3}$ ,… $m_{n}$ , the force exerted on mass $m_{1}$ is:

 $\vec{F_{1}} = \sum_{i = 2}^{n} {\vec{F}}_{1 i}$

THE GRAVITATIONAL AND THE INERTIAL MASS

When expressing the second law of Newton we use the inertial mass:

 ${\vec{F}}_{N E T} = m_{i n} \vec{a}$

When formulating the gravitation law, Newton was not sure that the mass of particles in this law is the same as their inertial mass. Let’s verify this issue.

We start by supposing that the mass in the gravitational law may be different from $m_{i n}$ . So, we call it $m_{g r}$ .

Let’s consider now a body in free fall close to earth surface. The earth will exert on it the gravitational force with magnitude:

 $F_{g r} = G \frac{m_{g r} M_{E a r t h}}{R_{E a r t h}^{2}}$

Here we assume that the body is close to the surface so that its distance form earth center is Earth ≅ $R_{E a r t h}$

As this is the net force exerted on the body we apply the second law of Newton

$F_{N E T} = m_{i n} a = F_{g r} = F_{g r} = G \frac{m_{g r} M_{E a r t h}}{R_{E a r t h}^{2}}$

So, we get

$m_{i n} a = m_{g r} (\frac{G M_{E a r t h}}{R_{E a r t h}^{2}}) = m_{g r} g$ , where $\frac{G M_{E a r t h}}{R_{E a r t h}^{2}} = g$

Then,

 $a = \frac{m_{g r}}{m_{i n}} g$

A big number of measurements show that the acceleration of free bodies is equal to $g = 9.8 m / s^{2}$ . This means that $m_{g r} / m_{i n} = 1$ , and $m_{i n} = m_{g r}$ .

So, the experiments confirm that the gravitational mass is the same as the inertial mass.

Let us apply the gravitation law for the force exerted by earth over a mass 1kg close to earth.

 $\vec{F} = - G \frac{M_{E a r t h}}{(R_{E a r t h} + h)^{2}} * \frac{\vec{R_{E a r t h}}}{R_{E a r t h}} \equiv \vec{g}$

So, the g-vector is equal to the gravitation force exerted on a mass 1kg.

By measuring the force exerted on the mass 1kg in different locations on the earth one gets a whole system of g-vectors (fig.2). The totality of these vectors forms the gravitational field of the earth.

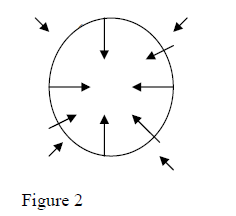
Note that the g-vector magnitude decreases with the increase of distance “h” from the earth but it is always directed versus the center of the earth. The gravitational field of the earth has a spherical symmetry.

In fact, it is not exactly spherical, because the model of earth as a uniform density sphere is not very precise. Now, the object weight is equal to gravitational force exerted by this field

 $\vec{W} = m \vec{g}$

So, the weight of the same object is a vector that is different in different points of gravitational field of the earth.

KEPLER’S LAWS ON PLANETARY MOTION

First law: The planets move on elliptic orbits around the sun that is located at one of its focuses.

The minor axis is long 2b and the major axis is long 2a. The closest distance to sun is called perihelion and the biggest distance to sun is called aphelion (fig.3).

Second law: The line sun- planet sweeps out equal areas for equal interval of times.

Third law: The square of the period of planet motion is proportional to the cube of average distance from the sun. Calculations show that the average of distance sun-planet is equal to half of major axis a. Then, satellite motion tells that

 $T^{2} = k a^{3}$  where

 $k_{s u n} = \frac{4 π^{2}}{G M_{s u n}}$

Note : Kepler’s laws are valid for elliptical paths of any planet around a central body; for example the moon moving around the earth but in this case

 $k_{E a r t h} = \frac{4 π^{2}}{G M_{E a r t h}}$

THE ENERGY OF PLANETS

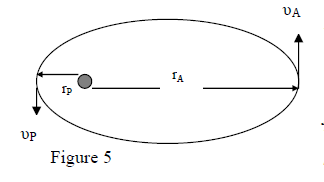
As the mass of other planets is much smaller than the mass of sun

we neglect their action on the motion of the studied planet. We consider that the system sun-planet is a conservative system, i.e. the forces originated from outside it are zero.

In these circumstances:

a) The torque of exterior force is zero and we can apply the principle for conservation of angular momentum.

b) The work done by Net exterior force is zero and we can apply the principle of energy conservation for the system sun-planet.

The principle of angular momentum conservation tells that $\vec{L_{A}} = \vec{L_{P}}$

or $\vec{r_{A}} \times \vec{p_{A}} = \vec{r_{P}} \times \vec{p_{P}}$

The equality of magnitudes brings to condition

$r_{A} p_{A} S i n 9 0^{o} = r_{P} p_{P} S i n 9 0^{o} \Rightarrow r_{A} m_{p l a n e t} v_{A} = r_{P} m_{p l a n e t} v_{P}$

So, we get

 $r_{A} v_{A} = r_{P} v_{P}$

The principle of energy conservation tells that that $E_{A} = E_{P}$

As the mechanical energy is E = K + U where

 $K = \frac{m_{p l} v_{p l}^{2}}{2}$   and

 $U = - G \frac{m_{p l} M_{S u n}}{r_{p l - s u n}}$

we get

 $\frac{m_{p l} v_{A}^{2}}{2} - G \frac{m_{p l} M_{S u n}}{r_{A}} = \frac{m_{p l} v_{P}^{2}}{2} - G \frac{m_{p l} M_{S u n}}{r_{P}}$

This gives, on cancelling $m_{p l}$ from the equation:

$\frac{v_{A}^{2}}{2} - G \frac{M_{S u n}}{r_{A}} = \frac{v_{P}^{2}}{2} - G \frac{M_{S u n}}{r_{P}}$

which leads to:

$2 G M_{S u n} (\frac{1}{r_{P}} - \frac{1}{r_{A}}) = v_{P}^{2} - v_{A}^{2}$

Now, we know $r_{A} v_{A} = r_{P} v_{P}$
and the fact that:

$r_{A} + r_{P} = 2 a$

Thus,

 $v_{A}^{2} = \frac{G M}{a} \frac{r_{P}}{r_{A}}$   and,

 $v_{P}^{2} = \frac{G M}{a} \frac{r_{A}}{r_{P}}$

Finally, by substituting one of this expressions at the expression of total energy (at perihelion or aphelion) we get

 $E = - G \frac{m_{p l} M_{S u n}}{2 a}$

See also

Dynamics of Circular Motion

EXERCISES

Exercises on Satellites and Binding Energy

Online Resources

Video: Incredible Inuit hunt mussels under sea ice

Newton's Law of Universal Gravitation

Contents

THE GRAVITATIONAL AND THE INERTIAL MASS

KEPLER’S LAWS ON PLANETARY MOTION

THE ENERGY OF PLANETS

EXERCISES

Online Resources

Navigation menu

Newton's Law of Universal Gravitation

THE GRAVITATIONAL AND THE INERTIAL MASS

KEPLER’S LAWS ON PLANETARY MOTION

THE ENERGY OF PLANETS

EXERCISES

Online Resources

Navigation menu

Search