Potential Energy
THE CONCEPT OF POTENTIAL ENERGY
Kreshnik Angoni
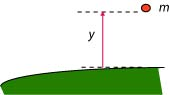
Consider an object at rest on the floor. As long as the application point of exerted forces (, ) is at the same location there is no work production. If one push the object at height ‘h’ and leaves it free, the object will fall, i.e. it will move vertically to h = 0. The force of “weight” will produce (positive) work
because its application point (Fig.1) is shifted by
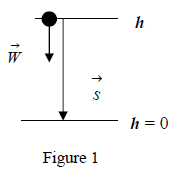
....... (1)
One can bring the object at the height ‘h’ by hand or by throwing it upward with the right initial velocity. No matter what way the object goes to the height ‘h’, once there, it is able to produce mechanical work.
One says that the object possesses a mechanical energy just because of the location. Essentially, this kind of energy is due to the gravity force which origin is the interaction earth – object.
So, when talking about this energy, it is more precise to refer to the configuration of earth - object system
(instead of object location).
In general terms:
Any kind of energy which is due to a system configuration is called potential energy.
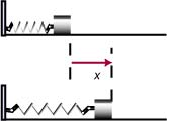
-Another example; A block tied at the free end of an elastic spring. If we extend the spring end by “x”, the restoring force produced by the spring will be directed towards the equilibrium position. When the block is returned at equilibrium position, the restoring force has produced the work:
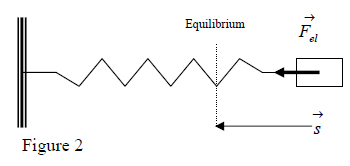
........ (2)
If the spring is left at rest, at its equilibrium, it does not possess any capacity to produce work. But, when it is extended (or compressed) , the same spring “is able” to produce work.
As the spring produces work this means that it does possess energy. As its ability to produce work depends only on its configuration (it has to be extended or compressed) this energy is due to configuration; So, it is a potential energy.
- In the two cases, initially, an external force (say hand’s force) does a positive work to shift the
system from an initial configuration ‘i’ to a final configuration ‘f’. Then, just because of being at “f”
configuration the system can provide work.
This capacity to produce work depends only on system configuration. So, it can be calculated by use of a configuration function (Function that depends only on the location (coordinates)); let’s call it . If we refer to values of this function at initial-final configurations and and remember that work brings the system from “i” to “f ” the simplest logical relation would be
........... (3) where

This relation fits perfectly with the logic that the positive external work () goes to increase the energy of the system on which this work is done (figure 3).
Note that this definition means that all the exterior work goes only for configuration changes and not for kinetic energy change of particles.
So, the system must be moved from configuration to the considered one by a constant speed (in practice very slowly) so that its kinetic energy remains unchanged.
- To avoid the ambiguity related to the external force, one prefers to refer the potential energy definition to the work by internal force.
The third law tells that during system transfer from to , the work by internal forces .
From relation (3), one gets to the actual definition for potential energy as:
= - ΔU = ........... (4)
- Note that the equation (4) is based on the difference ΔU = and not on the U- values.
This means that only ΔU has physical meaning (not U values).
The definition of U leaves “free choice” for the selection of configuration where U = 0.
Actually, one fixes to a selected initial configuration which depends from the considered problem.
Then, and we get to
....... (5)
Example: One selects when studying the displacement of an object from the floor up to a certain height, and when shifting it from the earth up. In both cases, the system is the
same “earth-object”, the internal force is the weight and
So, U = mgh
In case of the “spring block” system, one selects for undistorted spring (x = 0), the Hook’s force
is internal and
and
REMEMBER: In any case one has to define a potential energy function one refers to in equations (4,5).
NOTES:
- In general terms, a potential energy is due to interaction between system’s constituents.
- So, it does not make sense to talk about potential energy of a single object or particle alone.
- When one says that the potential energy of an object with mass ‘m’ at height ‘h ‘ is U = mgh , actually, this means
the energy of the ‘system object – earth due to their gravitational interaction.’
-The mechanical potential energy is due to gravitational and restoring (elastic) interactions.
- From a general point of view, one may define a potential energy only when the involved forces at
origin of this energy are conservative. In the following we explain the meaning of a conservative force.
TIPS AND TECHNIQUES
Helena Dedic
• The work done be conservative forces depends only on the initial and final position of the particle. This is why the potential energy is called the energy of position.
• The work-kinetic energy theorem can be also stated as follows:
• Definition of potential energy: The change of potential energy is defined as:
Systems of two interacting particles
| 2-body systems | potential energy | Choice of potential U = 0 | U | |
|---|---|---|---|---|
| mass m and earth near surface of earth |
Gravitational | at h = 0, Ug = 0 | mgh | |
| Spring-mass |
Spring | at x = 0, Usp = 0 | ||
| two masses and examples: rockets and satellites |
Gravitational | as |
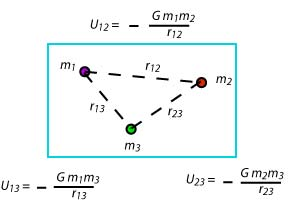
Systems of three or more interacting particles
(Total potential energy is equal to the sum of potential energies for each interaction )
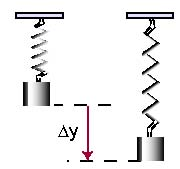
| spring-mass and earth |
|
| Gravitational interactions between three masses |
Why is gravitational potential energy negative?
- convention: gravitational potential energy is equal to zero when the gravitational force is equal to zero.
- When a system is held together by attractive forces the potential energy U is negative
Computing the gravitational potential energy
- for any problem involving rockets and satellites use formula
- for any problems involving motion close to earth surface () use formula
Determine the change of potential energy - problem solving strategy:
a. draw a diagram of the system to be considered
b. determine which conservative force(s) act in this system
c. determine the initial position and the final position of the system
d. if change in gravitaional potential energy, decide which formula to use for computation of gravitational potential energy
e. if there is a spring in the system, determine how is the displacement of a particle related to the extension of the spring
f. compute the change of the total potential energy of the system , where and = ½ .