Work and Energy
Kreshnik Angoni
INTRODUCTION
-Two concepts, work and energy, are widely used when studying mechanic’s problems because
they simplify the solutions of problems. Especially, in cases of problems containing forces that
change during object motion (Ex. spring’s force, friction force along a curved surface), one prefers
to use them instead of Newton’s laws.
- When lifting a body up in uniform way (zero acceleration) one has to exert a force with equal
magnitude to that of body weight. The everyday experience shows that:
• For same vertical lift, bigger the weight is, more muscular exertion is needed;
• For same weight, bigger the vertical lift is, more muscular exertion is needed;
So, one finds out that the quantity (weight * height change) can be a meaningful measure to
characterise the activity exerted by a “ source” that moves up an object from one level to higher
one. This is a first step, intuitively justified, toward the precise definition of mechanical work.
Concerning the energy, a first step approach would be to figure it out as the “capacity of a source to
furnish mechanical work”. This perception of the energy gives the indication that “the work is
equal to the change of energy in the source that furnishes it “ and it is good enough when we deal
only with mechanics phenomena. Note that introduces the other types of energy exchanges (heat,
electricity, chemical, nuclear..) by use of energy principle revealed in mechanics.
THE WORK DONE BY A CONSTANT FORCE
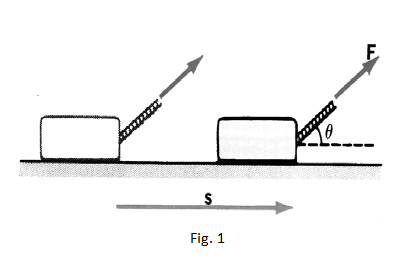
- One says that a constant force has done work only if the point where it is applied gets shifted.
If the object displacement is , one says that the force has achieved the work
W = . = Fs cosθ .......... (1)
θ (constant) is the angle between the direction of force and that of displacement.
Note that:
• The work is done by the source that exerts the force.
• If the displacement is zero, there is zero work even
though the source makes the effort (applies the force).
• Only the component of force along the displacement
direction achieves work. The force component
perpendicular to displacement achieves zero work
because in this case θ = .
- As the definition by scalar product shows, the work is a scalar physical quantity. Its unit is a
derived unit; in SI system its unit is the Joule (J) ;
1J = 1N*1m (force applied in displacement direction) ....... (2)
- One may calculate the work done by a constant force during a displacement
by using the components of those vectors in any Cartesian frame by the formula
W = . = . + . + = . + . + ....... (3)
Remember:
= Δx + Δy + Δz
Meanwhile, the numerical value of work does not depend on the inertial frame one may use to calculate it because the magnitudes of vectors , and the angle between them (expr. 1) do not
depend on the chosen frame.
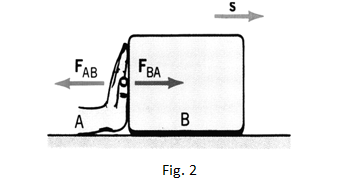
- The work done by or when a block slides on a horizontal plane (fig.2) is zero because they are both perpendicular to displacement vector. For the same reason the work done by centripetal forces is always zero.
When a set of forces , , ........, is acting on the same body that is displaced by , each of them achieves work independently of the others.
= .; = .; .........; = . (4)
Total work achieved on the body is:
= + ...... + = ( + + ...... ). = . (5)
= is the vector sum of all forces exerted on the body.
- From (1) we see that the work done by a force can be positive (if θ < ) or negative (if θ > ).
In figure 2, the hand “object A” pushes the block “object B” and shifts it by the displacement . This way, via the force exerted on B, the “object A” achieves the positive work
= . = = (6)
The third law of Newton tells that the block “object B “exerts on the hand “object A” a force with equal magnitude by opposite direction to
(7)
The work achieved by the block on the hand ( work done by force ) after the hand is shifted by is
= . = .= (8)
So, when the object A (hand) achieves a positive work to shift the object B (block), the object B(block) achieves the same amount of work (but negative) on the object A “source of force that displaces it”.
Work done by Frictional force
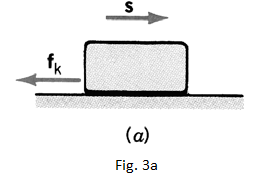
- When considering the work done by friction force one must verify carefully the displacement vector and the friction force directions before talking about the friction work. In the case of fig 3.a the friction has opposite direction versus displacement and
= . = = (9)
So, the friction achieves negative work on the block. The source of friction force is the floor. It is transmitted via the “ bonds” built in the interface between the block and floor.
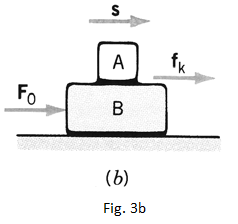
-In the case of figure 3.b, the force pushes the block B forward. The block A “due to its inertia
would tend to keep its position i.e. to slide left versus B”. Meanwhile, via friction forces, the block B
pushes on A to the right. In this case, the friction force has the same direction as displacement of A and it does a positive work on the block A.
Work Done by the Gravitational Force
- The work done by gravity force is an important example for clarifying some basic issues. Consider a block that is shifted up over an inclined plane under the effect of a pulling force (fig.4). We ignore the action of other forces, we concentrate on the work done by weight force. We select a frame of axes as shown and define the displacement vector. The selected system for axes is not good to study the motion by Newton's law but it allows inferring some important results and simplifies the calculation of work by use of formula (3). The components of gravity force in this system are (0,−mg) and those of the displacement are (Δx,Δy).
So, the formula (3) gives
...... (10)
When the block is shifted up, and the work done by gravity is negative. When the block slides down, and the work done by gravity is positive.
Note: If, at first, the block is shifted up from height to ; then left to slide down to , the total work done by gravity force is zero.
So: The work done by gravity depends only on initial and final heights and not on the path followed during the displacement.
In more general terms:
The work done by gravity is zero for any closed path (when final location falls on, or coincides with initial location).
Exercises on Work
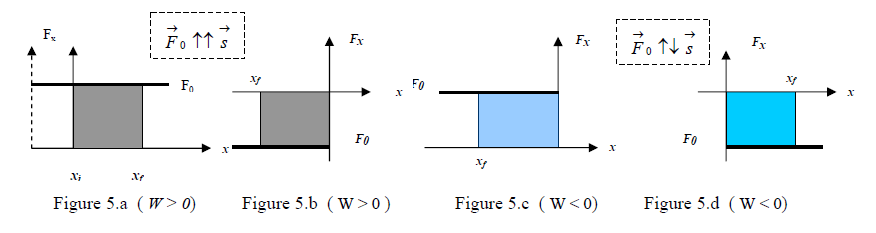
THE AREA TECHNIQUE FOR WORK CALCULATIONS IN ONE DIMENSIONAL SPACE
For a constant force in one dimension space, ,
and = () ....... (11)
This work is equal to the surface of shaded area under the graph f = f(x) shown in figure5.a. By setting the origin at , the area under the graph presents easily all possible sign combinations of a constant force and displacement vector. Note that area in first and third quadrant correspond to positive work while area in the second and fourth quadrant present negative work( fig.5.c, d).
- The area technique offers an easy way for work calculation in case of a variable force in a one dimension space. In this case, for each location of object under study there is a different exerted force. The elastic force of a spring is a good example of such type of force; when compressed or extended, an ideal (massless) spring, exerts at its moving end (see figure 6) the force
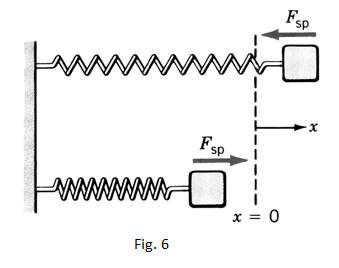
= - k * x ..(Hook’s law).... (12)
k [N/m] is the spring constant; x is the displacement of moving end from equilibrium.
Note that we have fixed and the displacement Δx = ( ) is equal to algebraic value of x.
When x > 0 (spring extended) the force is < 0 and when x < 0 (spring compressed) the force is > 0. So, in all cases, the spring’s force tends to restore the equilibrium position of spring. The forces that tend to bring the system to its equilibrium configuration are known as restoring forces.
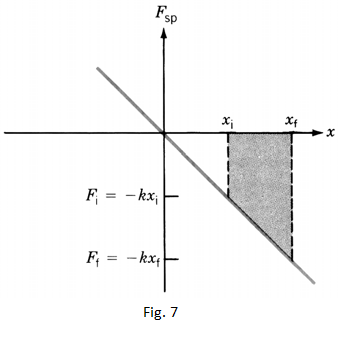
- The figure 7 shows the graph of relation (12). The work done by this force when its application point (spring end) is shifted from to is given by the area under the graph. By calculating this area through the difference of the two triangles’ areas one finds out that:
- = ....... (13)
-The expression (13) shows that the work done by a spring force depends only on initial and final positions of its moving end. Spring’s work is positive when the direction of its force is the same as that of displacement (shown in fig.6). This happens when the block is moving versus equilibrium point, i.e. . The work is negative when the direction of restoring force is opposite to that of displacement (not shown in fig.6).This happens when the block is moving away from equilibrium point, Also, for a full oscillation the spring’s work is zero because .
THE WORK – ENERGY THEOREM IN ONE DIMENSIONAL SPACE
-Consider a particle (object) with mass m in translational motion with acceleration a along the direction Ox under the effect of a net constant force directed along the same direction.

The work achieved by the force
for the displacement of the particle by Δx =
is:
= * ...... (14)
By using the relation between initial and final velocities one gets:
...... (15)
and by substituting in eq. (14):
....... (16)
- Definition: The quantity ....... (17)
is called the KINETIC ENERGY of the particle.
So, one can express the work done by the net force through the difference of K-values
= = ....... (18)
- Note that the definition of energy is a mathematical definition based on physic’s concept of work. Actually, the kinetic energy of particle is a measure of the work needed to increase its speed from zero to a given value v ( put Ki = 0 in eq(18) and get ). Equally, one may refer to the situation when the particle velocity is decreased from v to zero due to the stopping action from outside. In this case, and the net work done on the particle is negative
.
Remembering the third law, one infers that in this case, the particle spends its kinetic energy to achieve positive work on the surrounding medium. Note that this assertion fits with the idea about the energy as the capacity of this particle to provide work.
-The expression (17) shows that the numerical value of kinetic energy depends on the selected frame. In another inertial frame (in uniform motion), the velocity of particle is different and its kinetic energy has another value. This helps to keep in mind that the numerical value of kinetic energy depends on the selected frame and it is not very meaningful. Meanwhile, the changes of kinetic energy function do not depend on the frame where they are calculated and they do have
a precise physical meaning; they equal the net work achieved on the particle.
Note: We derived the work-energy theorem for the case of constant force acting in a one dimensional
space. This theorem remains true in case of variable forces acting in a two or
three-dimensional space, too.
Exercises on Work-Energy Theorem
POWER
- Suppose that we need to shift an object from point A to point B. This requires providing a certain amount of work and we have to choose between different sources that can provide this amount of work. Which one to chose? If we decide as selection principle “the source that can do the displacement quicker” we have to deal with another physical quantity; the mechanical power.
-The mechanical power is the rate at which a given work is done. If the “source” delivers a portion
of work ΔW in the time interval Δt, one says that it is delivering the average power
.......... (19)
The unit of power is the “Watt “
1W = 1J /1s ............(20)
The instantaneous mechanical power is defined as
............(21)
- If the “source” is acting on the object by the constant force during the infinitesimal shift
\vec{ds}, this means that it has provided the work
............(22)
If this happens during the infinitesimal time interval dt this means that the object was moving with
instantaneous velocity
.........(23)
from which we derive
After substitution in (22) we get
.........(24)
and finally, based on (21)
............(25)
The expression (25) is based on instantaneous vectors (force and velocity) . This means that the
power is a physical parameter that may change in time. But, if the force and velocity are constant
vectors, the power is constant, too. We say that the force is providing a constant power in time.
- From a formal point of view, the work done by the source of the force can be seen as the portion
of mechanical energy transferred from the “source” to the adjacent regions of space. This way,
the delivered power [watt] from a “source” would be
.......... (26)
where E [Joules] stands for the total mechanical energy of the “source” that provides the
mechanical power . The sign “ - “ in expression (26) is related to the fact that the energy of the
source is decreased when providing power while this power is positive in the sense that one use it to
do positive work.
SOME NOTES ABOUT ENERGY
Karen Tennennhouse
- Definition: A system means any group of objects we choose to examine. For a given system, we say that a force is internal iff it is exerted BY an object IN the system (on another object in the system). We say a force is external iff it is exerted BY an object which is NOT IN the system (on an object in the system).
- The definition of Work done by a constant force is:
which is also written as
The work measures the energy transfer caused by this force....... transfer from one object to another or from one energy form to another.
[The more general definition of work is:
.
For a one dimensional case, with parallel to the path, this integral can be found by taking the area of a graph of F versus ‘s’.
In this course, we will use this fact only once, to get our formula for elastic potential energy.] - Recall, the units of energy and work are , called Joules.
Equivalently, one Joule is the work done by one Newton of force acting parallel to one meter of displacement,i.e.
1 Joule = 1 N-m
(Caution: although Torques are also measured in N-m, they are not the same thing.)
Another unit of energy is the calorie (c).
1 cal = 4.18 Joules.
The food calorie (C) is 1 Cal = 1000 cals. - Some forms of Energy:
- Kinetic Energy (KE): A moving object has more energy than the same object had when at rest; the difference is called the kinetic energy. For speeds much less than the speed of light (including all problems in this course)
- Heat(Thermal Energy): In any object or substance, the microscopic particles, (atoms, electrons, etc.) are always in random motion or vibration. For the substance to be warmer (higher temperature) actually means that the average KE of these random microscopic motions is larger than when the substance is cooler.
- Light carries energy.
- Sound carries energy.
- Mass is energy! The famous equation tells us how much energy is equivalent to an amount ‘m’ of mass. c is the speed of light, m/s , so one kg of matter contains an enormous J of energy.
- Chemical Energy. This is a somewhat sloppy but still useful term. When we encounter chemical energy in a mechanics problem, most often it is either the chemical energy of fuels (wood, gasoline, etc.) or chemical energy of a person’s body being used up (to enable the person to move, keep warm, etc. or to do work on other objects.)
- Gravitational Potential Energy (GPE) is energy which has been “borrowed” when we did work against gravity, and which gravity will “pay back” if the object returns to its earlier position. Near the surface of the Earth, whenever an object moves upwards by an amount , its GPE increases by an amount . Similarly, if the object moves down, it loses GPE.
- Elastic Potential Energy is energy which has been “borrowed” when we did work against a spring or other elastic force. We will see that Elastic where k is the constant of the spring, and is the amount of stretch or compression, measured from the relaxed position of the spring.
- Electrostatic Potential Energy is energy which was borrowed when we did work against electrical forces (for example, by pushing two same-sign charges closer together.) You’ll learn more about electrostatic PE next year, in Physics NYB.
- We define the Total Mechanical Energy (written TME or just ME) as the sum of ( KE + all forms of potential energy.)
- But what is “potential energy”? Why do we talk about “gravitational PE”, but NOT “frictional PE” or “muscle PE”?
- Some forces, such as gravity, are “honest borrowers.” That is, whenever we seem to lose energy by doing work against gravity during a certain trip, we know that gravity will pay back exactly the same amount of energy if the object does the reverse trip back to its previous position. In fact, if no other forces are acting on the return trip, gravity will pay back this loan in the form of kinetic energy.
- A force with this property is called a conservative force. (Notice, not the same thing as conserved or conservation.)
- Each kind of conservative force has a corresponding form of potential energy
- Which forces are conservative?
Examples of Conservative Forces Examples of NON-Conservative Forces - Gravity, i.e. Weight
- Elastic tensions and compressions, i.e. those which obey Hooke’s law.
- The electrostatic (coulomb) force between electric charges.
- A very few others, that you’ll meet in future courses.
Almost everything that’s not in the left column. In particular: - Non-elastic tensions and compressions (e.g. ropes, normal force by most solids, etc.)
- Forces by muscles
- All forms of friction
- Roughly speaking, the mechanical forms of energy (KE and various potential energies) are related to “organized” motion of biggish objects. Non-mechanical forms, such as heat and chemical energy, are related to disorganized, random, microscopic events. The branch of Physics called Thermodynamics studies the interesting laws related to these ideas.
- The most general form of the energy law is: IF the net work done on a system by external forces is zero, THEN the total energy of the system (sum of all forms) remains constant. In our present course, we mostly use this law to solve simple problems, and for qualitative questions.
- There are two more specialized laws, which deal with the sub-group of mechanical energies.
In this course, we’ll solve most large, complex, energy problems using these two laws:
- IF the net work done by non-conservative forces is zero, THEN total mechanical energy stays constant.
- You can abbreviate this law as:
- If , then
- at all times.
- In general,the change in the mechanical energy equals the net work done by non-conservative forces,i.e.
- You can probably see that the second law includes the first one as a special case.
- Method for solving Large Energy Problems, using the mechanical energy laws:
- Choose the SYSTEM.
- CHECK: Does the net work done by non-conservative forces add up to zero?
At this step we need to think carefully about each force which is acting on the system (both external and internal.)- Is this force conservative or not?
- If not, does it do non-zero work?
- Write the LAW you plan to use:
If yes to B, plan to use at all times
If no to B, plan to use - Large, clear must include:
- Show and clearly label the different positions of the object.
- If the problem will involve GPE, choose and label the “zero-point”, where you will consider h = 0.
- Label with symbols the relevant distances and angles that you will use in your equations.
- NB: This is NOT an isolation diagram.
- Show and clearly label the different positions of the object.
- Write out the EQUATION applying your chosen law to this problem.
- This is where you put in the specific energy forms or etc. which are present in this problem.
- Use careful symbols and subscripts.
- If you’re using , your right-hand side may have one or several terms. The thinking you did for the “check” step will help you now.
- Make sure that any symbols for unknowns in your equation have been labelled in your main diagram.
- Substitute formulas and values. Solve. Express final answers.
- When sliding (kinetic) friction does work, it usually does negative work, making mechanical energy decrease. Some form of energy must increase, and usually it is heat (sometimes sound etc.) So for example, in a certain situation, if work done by friction is – 20 J, then heat or etc produced is + 20 J.
- We define power as the rate of energy transfer.
- Units of power are Joules/sec, usually called Watts.
- Average power by a certain force is
- Instantaneous power (derivative), but in our course, we are only using average or constant power.
- In almost all power problems in this course, just consider the energy changes in .
NOTES ON POTENTIAL ENERGY