Torque
Jump to navigation
Jump to search
Helena Dedic
If you need to understand the concept of center of mass, please see the link below:
CENTER OF MASS
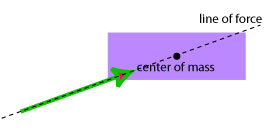
- A force causes a free object to move in a translational motion if it is applied at the centre of mass of the object or the line of force passes through the centre of mass.
- When a force is not applied at the centre of mass of a free object or when the line of force does not pass through the centre of mass then it causes this object to move in a complex way that involves both translation (i.e.: movement of the center of mass) as well as rotation (i.e.: movement around the center of mass.)
- OBSERVATIONS OF AN OBJECT:
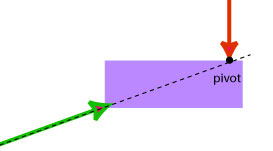
a) When a force acts at the pivot or when a line of force passes through the pivot,
the object does not begin to rotate.
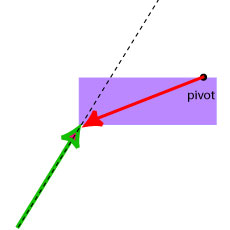
b) When a force acts at some distance from the pivot, the object begins to rotate.
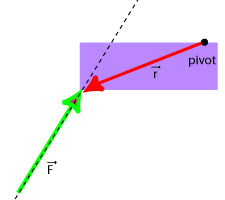
- Lever arm is a vector that points from the pivot to the point where the force acts.
- TORQUE: A cause of a change of the angular velocity (e.g.: a rotating wheel stops or it begins to rotate faster.
The symbol for torque is .
- Magnitude and direction of the torque: The magnitude of the torque depends on the magnitude of the lever arm, the magnitude of the force and the angle between these two vectors:
In special cases where the axis of rotation is given: The torque is positive when the torque causes the object to rotate in the counter-clockwise direction and negative when the torque causes the object to rotate in the clockwise direction.
- In general the torque is a vector product of the lever arm and the force:
Static Equilibrium Revisited
- An object is in static equilibrium if and only if and , where the net torque is the sum of all torques and the net force is the sum of all forces acting on an object.
- Static equilibrium problem solving strategy:
- Determine all forces acting on an object and draw an arrow for each force indicating:
- A point where this force is applied
- In which direction this force acts
- For each force:
- Identify the magnitude and the direction of lever arm
- Draw a diagram consisting of lever arm and force vectors and determine the angle between these two vectors
- Determine the direction of the torque and then compute its magnitude.
- Substitute into the equation
- Select the coordinate system
- Draw a free-body diagram
- Compute the components of the forces
- Substitute into the equations and
- Solve the system of three equations using the method of substitution